题目内容
15.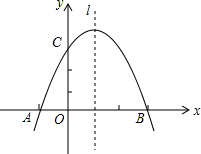 已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到.
已知:如图,二次函数的图象是由y=-x2向右平移1个单位,再向上平移4个单位所得到.(1)求二次函数的解析式;
(2)若点P是抛物线对称轴l上一动点,求使AP+CP最小的点P的坐标;
(3)M是y轴上一点,且△MAC是以AC为腰的等腰三角形,试求M点坐标.
分析 (1)根据二次函数图象“左加右减,上加下减”的平移规律即可得到新的二次函数的解析式和对称轴;
(2)连接BC,交对称轴于点P,连接AP、AC.点A关于对称轴x=1的对称点是点B (3,0),由几何知识可知,PA+PC=PB+PC为最小,依此求点P的坐标;
(3)当以AC为腰,A为顶点时和以AC为腰,C为顶点两种情况分类讨论即可确定点M的坐标.
解答 解:(1)二次函数的解析式:y=-(x-1)2+4,对称轴为直线x=1;
(2)连接BC,交对称轴于点P,连接AP、AC.
要使PA+PC最小.
∵点A关于对称轴x=1的对称点是点B(3,0),抛物线y=-x2+2x+3与y轴交点C的坐标为(0,3).
∴由几何知识可知,PA+PC=PB+PC为最小
设直线BC的解析式为y=kx+3,将B(3,0)代入3k+3=0,得k=-1.
∴y=-x+3,
∴当x=1时,y=2.
∴点P的坐标为(1,2).
(3)令y=-(x-1)2+4=0,
解得:x=3或x=-1,
∴A(-1,0),B(3,0),
令x=0,解得:y=3,
∴C(0,3),
∴AO=1,CO=3,
∴AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
如图,当以AC为腰,A为顶点时,此时CO=M1O,
∴M1的坐标为(0,-3),
当以AC为腰,C为顶点时,此时CM=AC,
即:CM2=AC=$\sqrt{10}$,CM3=AC=$\sqrt{10}$,
∴M2(0,3-$\sqrt{10}$),M3(0,3+$\sqrt{10}$)
点评 本题考查了二次函数综合题,涉及的知识点有:二次函数图象的几何变换,重点是找出平移变换的关系,轴对称-最短距离,两点之间线段最短.

练习册系列答案
相关题目
 已知如图,点D在CB延长线上,E在AB上,连接DE,若∠DEB=∠A,点B为DC中点.求证:DE=AC.
已知如图,点D在CB延长线上,E在AB上,连接DE,若∠DEB=∠A,点B为DC中点.求证:DE=AC.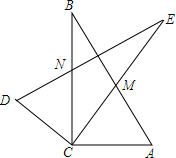 两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.
两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置,设两直角边BC、CE的夹角∠ECB=α,∠A=β.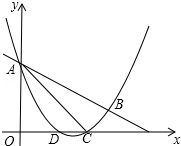 如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
如图,抛物线y=$\frac{1}{2}$x2+mx+n与直线y=-$\frac{1}{2}$x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).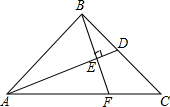 如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长
如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长 如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(d,0),其中a、b、d满足$\sqrt{a+1}$+|b-3|+(2-d)2=0,DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C. 如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.
如图,锐角△ABC的外接圆O.在BC边上取两点D、E使∠BAD=∠CAE,EM⊥AB于点M,EN⊥AC于点N,AD的延长线交⊙O于点P.求证:AP•MN=AB•AC•sin∠BAC.