题目内容
【题目】定义：有两个相邻内角和等于另两个内角和的一半的四边形称为半四边形，这两个角的夹边称为对半线.
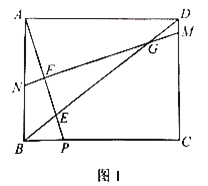
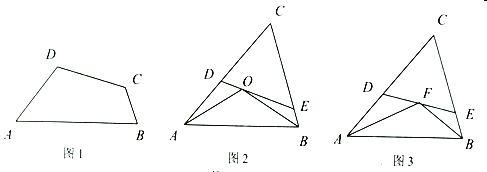
（1）如图1，在对半四边形
中，
，求
与
的度数之和；
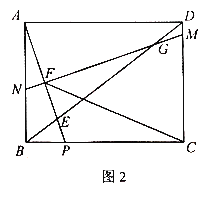
（2）如图2，
为锐角
的外心，过点的直线交
，
于点
，
，
，求证：四边形
是对半四边形；
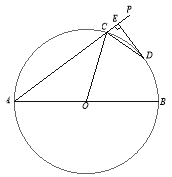
（3）如图3，在中，，分别是，上一点，
，
，
为
的中点，
，当
为对半四边形的对半线时，求的长.
【答案】（1）
；（2）详见解析；（3）5.25.
【解析】
（1）根据四边形内角和与对半四边形的定义即可求解；
（2）根据三角形外心的性质得
，得到
，从而求出
=60°，再得到
，根据对半四边形的定义即可证明；
（3）先根据
为对半四边形
的对半线得到，故可证明
为等边三角形，再根据一线三等角得到
，故
，列出比例式即可求出AD，故可求解AC的长.
（1）∵四边形内角和为
∴
，
∵
∴
=
则
，
∴
（2）连结
，由三角形外心的性质可得，
所以，
，
所以
，
则
在四边形中，，则另两个内角之和为
，
所以四边形为对半四边形；
（3）若为对半线，则，
∴
所以为等边三角形
∵
∴
又
∴
∵
∴，
∴
∵F为DE中点，
故
∴
∴
练习册系列答案
期末集结号系列答案
相关题目
