Question

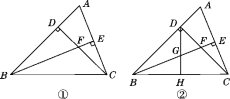
【题目】如图①，在等腰直角三角形BCD中，∠BDC＝90°， BF平分∠DBC，与CD相交于点F，延长BD到A，使DA＝DF.

(1)求证：△FBD≌△ACD；

(2)延长BF交AC于点E，且BE⊥AC，求证：CE＝BF；

(3)在(2)的条件下，H是BC边的中点，连接DH，与BE相交于点G，如图②. 试探索CE，GE，BG之间的数量关系，并证明你的结论．

Answer 1

【答案】（1）∵，

又∵；

∴，--------------------------3分

（2）∴，∴

又∵平分，∴

又∵，∴，

又∵

∴，∴

∴----------------------------- 7分

（3），,之间的数量关系为：

连结CG，∵，H是边的中点，

∴是的中垂线，

∴在中有：

∴-------------------------------------------------10分

【解析】

（1）由已知等腰直角三角形△DBC可推出DB=DC，且∠BDF=∠ADC=90°，与已知DA=DF通过SAS证得△FBD≌△ACD；
（2）先由（1）△FBD≌△ACD得出BF=AC，再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE，即得CE=AE=AC，从而得出结论；
（3）连接CG，由H是BC边的中点和等腰直角三角形△DBC得出BG=CG，再由直角三角形CEG得出CG2=CE2+GE2，从而得出CE，GE，BG的关系．

(1)证明：∵△BCD是等腰直角三角形，且∠BDC＝90°，∴BD＝CD，∠BDC＝∠CDA＝90°.

在△FBD和△ACD中，

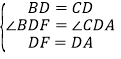
∴△FBD≌△ACD(SAS)．

(2)证明：∵BE⊥AC，

∴∠BEA＝∠BEC＝90°.

∵BF平分∠DBC，

∴∠ABE＝∠CBE，

又∵BE＝BE，

∴△ABE≌△CBE(ASA)，

∴AE＝CE.

∴CE＝AC.

由(1)知△FBD≌△ACD，

∴BF＝CA，

∴CE＝BF.

(3)解：BG2＝GE2＋CE2.证明如下：连接CG，

∵H是BC边的中点，BD＝CD，

∴HD垂直平分BC，

∴BG＝CG(线段垂直平分线上的点到这条线段两个端点的距离相等)．

∵BE⊥AC，

∴在Rt△CEG中，CG2＝GE2＋CE2，

∴BG2＝GE2＋CE2.