题目内容
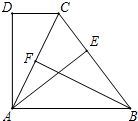
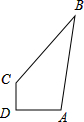 如图:∠ADC=90°,AD=12,CD=9,AB=39,BC=36,求四边形ABCD的面积.
如图:∠ADC=90°,AD=12,CD=9,AB=39,BC=36,求四边形ABCD的面积.分析:先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△BCA的形状,再利用三角形的面积公式求解即可.
解答: 解:∵∠D=90°,AD=9,CD=12,
解:∵∠D=90°,AD=9,CD=12,
∴AC=15,
在△BCA中,
BC2+AC2=152+362=392=AB2,
∴△BCA是直角三角形,
∴S四边形ABCD=
AC•BC+
AD•CD,
=
×9×12+
×36×15,
=54+270,
=324.
答:四边形ABCD的面积是324.
 解:∵∠D=90°,AD=9,CD=12,
解:∵∠D=90°,AD=9,CD=12,∴AC=15,
在△BCA中,
BC2+AC2=152+362=392=AB2,
∴△BCA是直角三角形,
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=54+270,
=324.
答:四边形ABCD的面积是324.
点评:本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
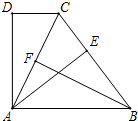 已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.
已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.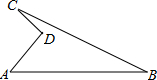 如图,∠ADC=90°,AD=4,CD=3,AB=13,BC=12,则这个图形的面积为
如图,∠ADC=90°,AD=4,CD=3,AB=13,BC=12,则这个图形的面积为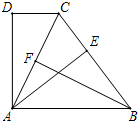 已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.
已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.