题目内容
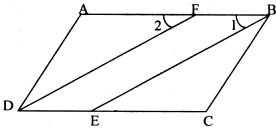
已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.
(1)求证:∠AFB=90°;
(2)求证:△ADC≌△AEC;
(3)连接DE,试判断DE与BF的位置关系,并证明.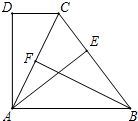
(1)求证:∠AFB=90°;
(2)求证:△ADC≌△AEC;
(3)连接DE,试判断DE与BF的位置关系,并证明.

(1)证明:∵BA=BC,F是AC的中点(已知),
∴BF⊥AC(等腰三角形的三线合一).(1分)
∴∠AFB=90°(垂直的定义).(1分)
(2)证明:∵AE⊥BC(已知),
∴∠AEC=90°(垂直的定义).
∵∠ADC=90°(已知),
∴∠ADC=∠AEC(等量代换).(1分)
∵DC∥AB(已知),
∴∠DCA=∠CAB(两直线平行,内错角相等).
∵BA=BC(已知),
∴∠ECA=∠CAB(等边对等角).
∴∠DCA=∠ECA(等量代换).(1分)
在△ADC和△AEC中,
∴△ADC≌△AEC(AAS).(1分)
(3)DE与BF平行.(1分)
证明:设DE交AC于点H,
∵△ADC≌△AEC(已证),
∴AD=AE,∠DAH=∠EAH(全等三角形对应边相等、对应角相等).(1分)
∴BH⊥DE(等腰三角形的三线合一).(1分)
∴∠AHE=90°(垂直的定义)
∵∠AFB=90°(已证),
∴∠AFB=∠AHE(等量代换).(1分)
∴DE∥BF(同位角相等,两直线平行).
∴BF⊥AC(等腰三角形的三线合一).(1分)
∴∠AFB=90°(垂直的定义).(1分)
(2)证明:∵AE⊥BC(已知),
∴∠AEC=90°(垂直的定义).
∵∠ADC=90°(已知),
∴∠ADC=∠AEC(等量代换).(1分)
∵DC∥AB(已知),
∴∠DCA=∠CAB(两直线平行,内错角相等).
∵BA=BC(已知),
∴∠ECA=∠CAB(等边对等角).
∴∠DCA=∠ECA(等量代换).(1分)
在△ADC和△AEC中,
|
∴△ADC≌△AEC(AAS).(1分)
(3)DE与BF平行.(1分)
证明:设DE交AC于点H,
∵△ADC≌△AEC(已证),
∴AD=AE,∠DAH=∠EAH(全等三角形对应边相等、对应角相等).(1分)
∴BH⊥DE(等腰三角形的三线合一).(1分)
∴∠AHE=90°(垂直的定义)
∵∠AFB=90°(已证),
∴∠AFB=∠AHE(等量代换).(1分)
∴DE∥BF(同位角相等,两直线平行).

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
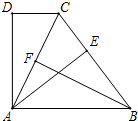 已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.
已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点. 已知:如图,A、D、B三点在同一条直线上,△ADC、△BDO为等腰三角形,AO、BC的大小关系和位置关系分别如何?证明你的结论.
已知:如图,A、D、B三点在同一条直线上,△ADC、△BDO为等腰三角形,AO、BC的大小关系和位置关系分别如何?证明你的结论.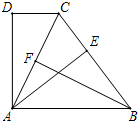 已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.
已知:如图,∠ADC=90°,DC∥AB,BA=BC,AE⊥BC,垂足为点E,点F为AC的中点.