题目内容
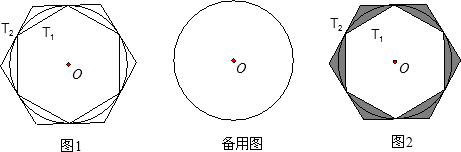
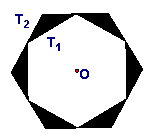
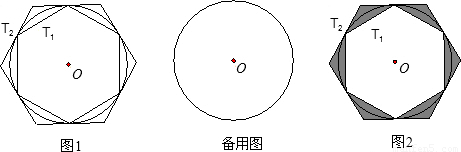
 如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为
如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为
- A.


- B.


- C.


- D.


A
分析:由于六边形ABCDEF是正六边形,所以∠AOB=60°,故△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,OG=OA•sin60°,再根据S阴影=S△OAB-S扇形OMN,进而可得出结论.
解答: 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA•sin60°=2× =
= ,
,
∴S阴影=S△OAB-S扇形OMN= ×2×
×2× -
- =
= -
- .
.
故选A.
点评:本题考查的是正多边形和圆,根据正六边形的性质求出△OAB是等边三角形是解答此题的关键.
分析:由于六边形ABCDEF是正六边形,所以∠AOB=60°,故△OAB是等边三角形,OA=OB=AB=2,设点G为AB与⊙O的切点,连接OG,则OG⊥AB,OG=OA•sin60°,再根据S阴影=S△OAB-S扇形OMN,进而可得出结论.
解答:
 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OA•sin60°=2×
 =
= ,
,∴S阴影=S△OAB-S扇形OMN=
 ×2×
×2× -
- =
= -
- .
.故选A.
点评:本题考查的是正多边形和圆,根据正六边形的性质求出△OAB是等边三角形是解答此题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目