Question

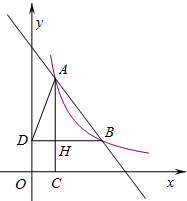（2012•镇赉县模拟）如图，在直角坐标平面内，函数y=

m

x

（x＞0，m是常数）的图象经过A（1，4），B（a，b），其中a＞1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，BD与AC交于点H，连接AD．
（1）若△ABD的面积为4，求m值及点B的坐标．
（2）在（1）的条件下，求直线AB的函数解析式．

Answer 1

分析：（1）代入点A的坐标可求出m的值，根据函数经过点B（a，b）及△ABD的面积为4，可求出a和b的值．
（2）根据A、B的坐标，利用待定系数法可求出AB的函数解析式．

解答：解：（1）∵函数y=

m

x

的图象经过点A（1，4），
∴m=4，即函数解析式为y=

4

x

，
∵函数y=

4

x

经过点B（a，b），
∴b=

4

a

①，
又∵S△ABD=

1

2

DB×AH=

1

2

a（4-b）=4②，
∴联合①②可得a=3，b=

4

3

．
即可得点B的坐标为（3，

4

3

）．
（2）设直线AB的解析式为y=kx+b，将A、B的坐标代入可得：

k+b=4 3k+b= 4 3

，
解得：

k=- 4 3 b= 16 3

，
故直线AB的解析式为y=-

4

3

x+

16

3

．

点评：本题考查了待定系数法求反比例函数解析式、三角形的面积，要注意掌握待定系数法的运用及点的坐标与线段长度的转化，难度一般．