Question

【题目】如图，在平面直角坐标系中，已知直线与反比例函数的图像交于点A，且点A的横坐标为1，点B是x轴正半轴上一点，且⊥．

（1）求反比例函数的解析式；

（2）求点B的坐标；

（3）先在的内部求作点P，使点P到的两边OA、OB的距离相等，且PA=PB.（不写作法，保留作图痕迹，在图上标注清楚点P）

Answer 1

【答案】（1）;（2）点的坐标是；（3）见解析.

【解析】

（1）设点的坐标为（1，）先求出点A纵坐标，再求出反比例系数k即可得出反比例函数的解析式；
（2）过点A作AC⊥OB⊥，在RT△AOC中先求出OA，再在RT△AOB中求出OB即可解决问题；

（3）画出∠AOB的平分线OM，线段AB的垂直平分线EF，OM与EF的交点就是所求的点P，设点P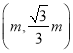，根据PA2=PB2，列出方程即可解决问题．

解：（1）由题意，设点的坐标为（1，），

∵点在正比例函数的图像上，

∴.

∴点的坐标为.

∵点在反比例函数的图像上，

∴，解得.

∴反比例函数的解析式为.

（2）过点作⊥，垂足为点，

可得，.

∵⊥，

∴∠°．

由勾股定理，得．

∴．

∴∠°.

∴∠°.

∵⊥，

∴∠°.

∴∠°.

∴.

∴.

∴点的坐标是.

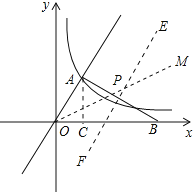
（3）如图所示.

如图作∠AOB的平分线OM，AB的垂直平分线EF，OM与EF的交点就是所求的点P，
∵∠POB=30°，
∴可以设点P坐标为，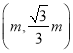

∵PA2=PB2，

解得m=3，
∴点P的坐标是