题目内容
已知线段AB=4,点C是其黄金分割点,且AC>BC,则AC-BC= .
考点:黄金分割
专题:计算题
分析:根据黄金分割的定义得到AC=
AB=2
-2,再计算BC的长,然后计算AC-BC.
| ||
| 2 |
| 5 |
解答:解:∵点C是其黄金分割点,且AC>BC,
∴AC=
AB=
×4=2
-2
BC=AB-AC=4-(2
-2)=6-2
,
∴AC-BC=2
-2-(6-2
)=4
-8.
故答案为4
-8.
∴AC=
| ||
| 2 |
| ||
| 2 |
| 5 |
BC=AB-AC=4-(2
| 5 |
| 5 |
∴AC-BC=2
| 5 |
| 5 |
| 5 |
故答案为4
| 5 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列命题中,真命题的个数是( )
①平分弦的直径垂直于弦;②圆内接平行四边形必为矩形;③圆内接四边形ABCD的四个内角之比可以是∠A:∠B:∠C:∠D=1:2:3:4;④不在同一条直线上的三个点确定一个圆.
①平分弦的直径垂直于弦;②圆内接平行四边形必为矩形;③圆内接四边形ABCD的四个内角之比可以是∠A:∠B:∠C:∠D=1:2:3:4;④不在同一条直线上的三个点确定一个圆.
| A、4 | B、3 | C、2 | D、1 |
cos60°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
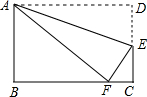 把一张长方形纸片(长方形ABCD)按如图所示方式折叠,折痕为AE,使点D落在BC边的点F处,若AB=8cm,BC=10cm,则重叠部分△AEF的面积是
把一张长方形纸片(长方形ABCD)按如图所示方式折叠,折痕为AE,使点D落在BC边的点F处,若AB=8cm,BC=10cm,则重叠部分△AEF的面积是 如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有
如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有 如图,在平面直角坐标系中,抛物线y=ax2+bx+4与y轴交于A点,与x轴交于B、C两点,∠ABO=∠OAC,BC=6,求抛物线解析式.
如图,在平面直角坐标系中,抛物线y=ax2+bx+4与y轴交于A点,与x轴交于B、C两点,∠ABO=∠OAC,BC=6,求抛物线解析式.