题目内容
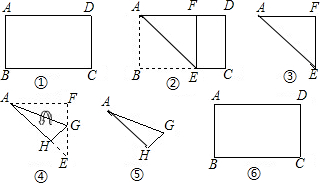
矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 ▲ ;


解析:如图所示,设PF⊥CD,
∵BP=FP,
由翻折变换的性质可得BP=B′P,
∴FP=B′P,
∴FP⊥CD,
∴B′,F,P三点构不成三角形,
∴F,B′重合分别延长AE,DC相交于点G,
∵AB平行于CD,
∴∠BAG=∠AGC,
∵∠BAG=∠B′AG,AGC=∠B′AG,
∴GB′=AB′=AB=5,
∵PB′(PF)⊥CD,
∴PB′∥AD,
∴△ADG∽△PB′G,
∵Rt△ADB′中,AB′=5,AD=3,
∴DB′=4,DG=DB′+B′G=4+5=9,
∴△ADG与△PB′G的相似比为9:5,
∴AD:PB′=9:5,
∵AD=3,
∴PB′=![]() ,即相等距离为
,即相等距离为![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
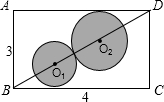 如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )
如图,矩形纸片ABCD中,AB=3cm,BC=4cm,若要在该纸片中剪下两个外切的圆⊙O1和⊙O2,要求⊙O1和⊙O2的圆心均在对角线BD上,且⊙O1和⊙O2分别与BC、AD相切,则O1O2的长为( )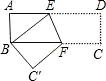 如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为
如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为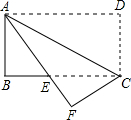 如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.
如图,在矩形纸片ABCD中,将矩形纸片沿着对角线AC折叠,使点D落在点F处,设AF与BC相交于点E.