题目内容
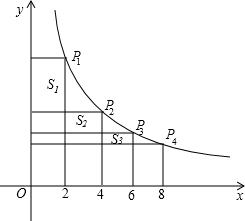
如图,在函数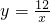 (x>0)的图象上,有点P1,P2,P3,…,Pn,Pn+1,若P1的横坐标为2,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1=________,S1+S2+S3+…+Sn=________.(用n的代数
(x>0)的图象上,有点P1,P2,P3,…,Pn,Pn+1,若P1的横坐标为2,且以后每点的横坐标与它前面一个点的横坐标的差都为2,过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1=________,S1+S2+S3+…+Sn=________.(用n的代数 式表示)
式表示)
6 
分析:由已知得出,点P1,P2,P3,…,Pn,Pn+1的横坐标分别为,2,4,6,…,2n,2(n+1),再由函数y= ,得各点的纵坐标分别为:
,得各点的纵坐标分别为: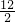 ,
, ,
, ,…,
,…, ,
, .由此通过观察求出S1,且表示出S2,S3,…Sn.从而求出S1+S2+S3+…+Sn.
.由此通过观察求出S1,且表示出S2,S3,…Sn.从而求出S1+S2+S3+…+Sn.
解答:由已知图象得:
点P1的坐横标a=2,代入y= ,得:
,得:
y=6,即点P1的坐标为(2,6)
同理得点P2的坐标为(4,3)
那么S1=2×6-(4-2)×3=6.
观察图象及已知函数y= ,
,
所以点Pn的横坐标为2n,纵坐标为 即
即 .
.
点Pn+1的坐标为的横坐标为2(n+1),纵坐标为 .
.
根据图象和得到的规律得:
S1=2×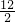 -2×
-2× ,S2=2×
,S2=2× -2×
-2× ,S3=2×
,S3=2× -2×
-2× ,S4=2×
,S4=2× -2×
-2× ,…,Sn=2×
,…,Sn=2× -2×
-2× ,
,
所以,S1+S2+S3+…+Sn=2×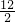 -2×
-2× +2×
+2× -2×
-2× +2×
+2× -2×
-2× +…+2×
+…+2× -2×
-2×
=2×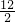 -2×
-2× =12-
=12- =
= .
.
故答案分别为:6, .
.
点评:此题考查的知识点是反比例函数思想,解答此题的关键是由已知得出点P1,P2,P3,…,Pn,Pn+1的横坐标,再由再由函数y= ,得出各点的纵坐标,再得出答案.
,得出各点的纵坐标,再得出答案.

分析:由已知得出,点P1,P2,P3,…,Pn,Pn+1的横坐标分别为,2,4,6,…,2n,2(n+1),再由函数y=
 ,得各点的纵坐标分别为:
,得各点的纵坐标分别为: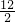 ,
, ,
, ,…,
,…, ,
, .由此通过观察求出S1,且表示出S2,S3,…Sn.从而求出S1+S2+S3+…+Sn.
.由此通过观察求出S1,且表示出S2,S3,…Sn.从而求出S1+S2+S3+…+Sn.解答:由已知图象得:
点P1的坐横标a=2,代入y=
 ,得:
,得:y=6,即点P1的坐标为(2,6)
同理得点P2的坐标为(4,3)
那么S1=2×6-(4-2)×3=6.
观察图象及已知函数y=
 ,
,所以点Pn的横坐标为2n,纵坐标为
 即
即 .
.点Pn+1的坐标为的横坐标为2(n+1),纵坐标为
 .
.根据图象和得到的规律得:
S1=2×
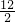 -2×
-2× ,S2=2×
,S2=2× -2×
-2× ,S3=2×
,S3=2× -2×
-2× ,S4=2×
,S4=2× -2×
-2× ,…,Sn=2×
,…,Sn=2× -2×
-2× ,
,所以,S1+S2+S3+…+Sn=2×
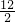 -2×
-2× +2×
+2× -2×
-2× +2×
+2× -2×
-2× +…+2×
+…+2× -2×
-2×
=2×
 -2×
-2× =12-
=12- =
= .
.故答案分别为:6,
 .
.点评:此题考查的知识点是反比例函数思想,解答此题的关键是由已知得出点P1,P2,P3,…,Pn,Pn+1的横坐标,再由再由函数y=
 ,得出各点的纵坐标,再得出答案.
,得出各点的纵坐标,再得出答案. 
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在函数y=
如图,在函数y=| 1 |
| x |
| A、SA<SB<SC |
| B、SA>SB>SC |
| C、SA=SC=SB |
| D、SA<SC<SB |
 如图:在函数y=
如图:在函数y=| 4 |
| x |
| A、矩形BCFG和矩形GAEP面积相等 |
| B、矩形FOEP和正方形COAB面积相等 |
| C、点B的坐标是(4,4) |
| D、图象关于过O、B两点的直线对称 |
 如图,在函数中 y=
如图,在函数中 y=| 1 |
| x |
| A、S1>S2>S3 |
| B、S1<S2<S3 |
| C、S1<S3<S2 |
| D、S1=S2=S3 |
 式表示)
式表示) (2013•眉山)如图,在函数y1=
(2013•眉山)如图,在函数y1=