题目内容
20.先化简,再求值:($\frac{3}{x-2}$+$\frac{2}{x+2}$)÷$\frac{5{x}^{2}+2x}{{x}^{2}-4}$,其中x是满足-2≤x≤2的整数.分析 先根据分式混合运算的法则把原式进行化简,再选取x的值代入进行计算即可.
解答 解:原式=$\frac{3(x+2)+2(x-2)}{(x-2)(x+2)}$÷$\frac{x(5x+2)}{(x+2)(x-2)}$
=$\frac{3x+6+2x-4}{(x-2)(x+2)}$÷$\frac{x(5x+2)}{(x+2)(x-2)}$
=$\frac{5x+2}{(x-2)(x+2)}$•$\frac{(x+2)(x-2)}{x(5x+2)}$
=$\frac{1}{x}$,
∵x是满足-2≤x≤2的整数,
∴x可以取1,-1,
∴当x=1时,原式=1;
当x=-1时,原式=-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
11.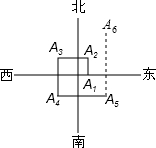 如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
 如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )| A. | (9,12) | B. | (9,9) | C. | (9,6) | D. | (9,3) |
8.”造林见林,见林见效”这是退耕还林、造林的基本要求,更是农民的朴实愿望,四川省林业厅副厅长包建华说,退耕还林直补给退耕农户带来实惠,累计兑现政策性补助资金331.92亿元,户均5500元.将331.92亿用科学记数法表示为( )
| A. | 3.3192×108 | B. | 3.3192×109 | C. | 3.3192×1010 | D. | 3.3192×1011 |
5.计算:22012-(-2)2013的结果是( )
| A. | 3×22012 | B. | 24025 | C. | -22012 | D. | ($\frac{1}{2}$)2012 |
12.若关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$无解,则m的值为( )
| A. | -l.5 | B. | 1 | C. | -l.5或2 | D. | -0.5或-l.5 |
9.下列各数能用科学记数法表示为3.14×10-3的是( )
| A. | 0.000314 | B. | 0.00314 | C. | 0.0314 | D. | 3140 |
10.方程与下列哪个方程组合,使得方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$( )
| A. | 3x+2y=7 | B. | -2x+y=-3 | C. | 6x+y=8 | D. | 以上都不对 |
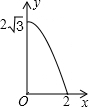
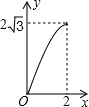
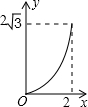
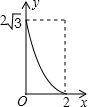
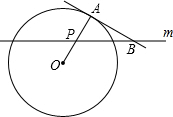 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )