题目内容
【题目】在平面直角坐标系中点![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点且
轴上的点且![]() 点的坐标是
点的坐标是![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,是靠近点
上,是靠近点![]() 的三等分点.点
的三等分点.点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标是__________.
的坐标是__________.
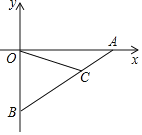
【答案】(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2)
)或(0,-2)
【解析】
根据条件可得AC=2,过点C作CD⊥OA,由勾股定理得到OC=![]() ,再分以下三种情况求解:①当OP=OC时,可直接得出点P的坐标为(0,
,再分以下三种情况求解:①当OP=OC时,可直接得出点P的坐标为(0,![]() )或(0,-
)或(0,-![]() );②当PO=PC时,点P在OC的垂直平分线PE上,先求出直线OC的解析式,从而可求出直线PE的解析式,最后可求得P(0,-
);②当PO=PC时,点P在OC的垂直平分线PE上,先求出直线OC的解析式,从而可求出直线PE的解析式,最后可求得P(0,-![]() );③当CO=CP时,根据OP=2|yC|=2×1=2,求得P(0,-2).
);③当CO=CP时,根据OP=2|yC|=2×1=2,求得P(0,-2).
解:∵点B坐标是(0,-3),∠OAB=30°,
∴AB=2×3=6,AO=3![]() ,
,
∵点C在线段AB上,是靠近点A的三等分点,
∴AC=2,
过点C作CD⊥OA于D,
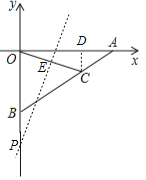
∴CD=![]() AC=1,
AC=1,
∴AD=![]() CD=
CD=![]() ,
,
∴OD=OA-AD=3![]() -
-![]() =2
=2![]() ,
,
∴OC=![]() .
.
∵△OCP为等腰三角形,分以下三种情况:
①当OP=OC=![]() 时,点P的坐标为(0,
时,点P的坐标为(0,![]() )或(0,-
)或(0,-![]() );
);
②当PO=PC时,点P在OC的垂直平分线PE上,其中E为OC的中点,
∴点E的坐标为(![]() ,-
,-![]() ),
),
设直线OC的解析式为y=k1x,将点C(2![]() ,-1)代入得k1=-
,-1)代入得k1=-![]() ,
,
则可设直线PE的解析式为y=k2x+b,则k1·k2=-1,∴k2=2![]() ,
,
∴将点E(![]() ,-
,-![]() )代入y=2
)代入y=2![]() x+b,得b=-
x+b,得b=-![]() ,
,
∴P(0,![]() ),
),
③当CO=CP时,OP=2|yC|=2×1=2,
∴P(0,-2),
综上所述,当△OCP为等腰三角形时,点P的坐标为(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2),
)或(0,-2),
故答案为:(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2).
)或(0,-2).

练习册系列答案
相关题目