Question

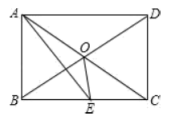
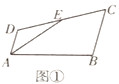
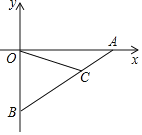
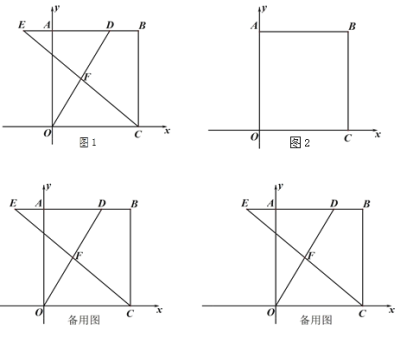
【题目】矩形OABC的顶点O与坐标原点重合，点B的坐标为(6，8)，动点D、E分别从点B、A同时出发，沿射线BA运动，点D、E的运动速度均为每秒2个单位，设D、E的运动时间为t秒．连接OD、CE交于点F．

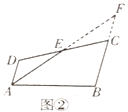
（1）如图1，求点F的纵坐标；

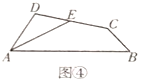
（2）若点G为OA的中点，在点D、E运动过程中，设△GEF的面积为y，求y与t的关系式；

（3）在（2）的条件下，连接BG，线段BG、OD交于点K，若，坐标平面内是否存在点M，使以D、E、K、M为顶点的四边形为平行四边形，如果存在，请求出点M的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）4 （2） （3）存在，点M的坐标为

【解析】

（1）根据矩形的性质可证明，即可得，从而求出点F的纵坐标；

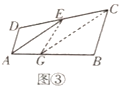
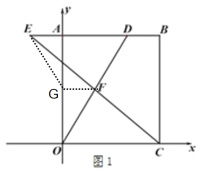
（2）如图，连接EG、FG，根据三角形面积公式求解即可；

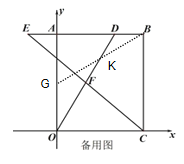
（3）连接BG，线段BG、OD交于点K，根据，求出t的值，即可得到点E、点D的坐标，再联立直线GB和直线OD的解析式求出K的坐标，根据平行四边形对角线互相平分求解出M的坐标即可．

（1）∵动点D、E分别从点B、A同时出发，沿射线BA运动，点D、E的运动速度均为每秒2个单位

∴

∵四边形OABC是矩形

∴

∴

在△EDF和△COF中

∴

∴

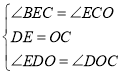
∴点F的纵坐标为 ；

（2）如图，连接EG、FG

∵

∴

∵

∴

∴

∵G是OA的中点

∴

∴

∴

∴；

（3）存在，连接BG，线段BG、OD交于点K，

∵，

∵

∴

∴，

解得

∵连接BG，线段BG、OD交于点K

∴

∴

∴

设直线GB的解析式为

将代入中

解得

∴

设直线OD的解析式为

将代入中

解得

联立方程得

解得

将代入中

∴

∴

设

①对角线为KE时

解得

∴

②对角线为DE时

解得

∴

③对角线为KD时

解得

∴

故存在，点M的坐标为．