题目内容
17．
如图，将矩形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线F处．若AB=6，AD=8，则ED的长为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 2 |
分析 首先利用勾股定理计算出AC的长，再根据折叠可得△DEC≌△FEC，设ED=x，则FE=x，AF=AC-CF=4，AE=8-x，再根据勾股定理可得方程42+x2=（8-x）2，再解方程即可．
解答 解：在矩形ABCD中，AB=6，AD=8，
∴DC=6，
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=10，
根据折叠可得：△DEC≌△FEC，
∴FC=DC=6，DE=FE，
设ED=x，则FE=x，AF=AC-CF=4，AE=8-x，
在Rt△AEF中：（AF）2+（EF）2=AE2，
42+x2=（8-x）2，
解得：x=3，
故选A
点评 此题主要考查了图形的翻折变换，以及勾股定理的应用，关键是掌握折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
10．如果一次函数y=kx+2k+1的图象经过第一、二、三象限，则k的取值范围是（ ）
| A． | k＞0 | B． | k＞-$\frac{1}{2}$ | C． | k＜0 | D． | -$\frac{1}{2}$＜k＜0 |
11．下列计算正确的是（ ）
| A． | x+x=x2 | B． | x•x=2x | C． | （x3）2=x5 | D． | x3÷x-1=x4 |
如图，已知：在?ABCD中，AB=AD=2，∠DAB=60°，F为AC上一点，E为AB中点，则EF+BF的最小值为$\sqrt{3}$．
和二次函数
的图象可能为（ ）
B. 
C. 
D. 
2．下列各组数中不能作为直角三角形的三边长的是（ ）
| A． | 6、8、9 | B． | 7、24、25 | C． | 1.5、2、2.5 | D． | 9、12、15 |
9．
若实数a、b在数轴上对应点的位置如图所示，则$\sqrt{{a}^{2}-2ab+{b}^{2}}$可化简为（ ）
若实数a、b在数轴上对应点的位置如图所示，则$\sqrt{{a}^{2}-2ab+{b}^{2}}$可化简为（ ）| A． | a+b | B． | a-b | C． | b-a | D． | -a-b |
6．下列调查中，适合采用全面调查的是（ ）
| A． | 了解我国各地中学多媒体的使用情况 | |
| B． | 测试我国某新型导弹的威力 | |
| C． | 对某商场防火安全的调查 | |
| D． | 对今年全国各地酒店“杜绝浪费，提倡节约”的调查 |
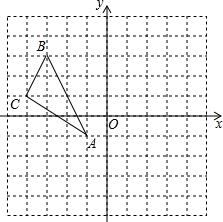如图，在平面直角坐标系中，△ABC的三个顶点分别为A（-1，-1），B（-3，3），C（-4，1）