题目内容
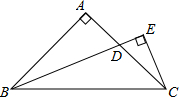 如图,△ABC为等腰直角三角形,∠A=90°,BD是∠ABC的平分线,作CE⊥BD的延长线于点E,求证:BD=2CE.
如图,△ABC为等腰直角三角形,∠A=90°,BD是∠ABC的平分线,作CE⊥BD的延长线于点E,求证:BD=2CE.考点:全等三角形的判定与性质,等腰三角形的判定与性质,等腰直角三角形
专题:证明题
分析:延长CE、BA相交于点F.可以证明Rt△ABD≌Rt△ACF,得出BD=CF,再证明△BCE≌△BFE得到CE=EF,就可以得出结论.
解答:解:延长CE、BA相交于点F.
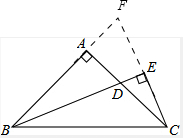
∵∠EBF+∠F=90°,∠ACF+∠F=90°
∴∠EBF=∠ACF.
在△ABD和△ACF中,
,
∴△ABD≌△ACF(ASA)
∴BD=CF
在△BCE和△BFE中,
,
∴△BCE≌△BFE(ASA)
∴CE=EF
∴BD=CF=2CE.

∵∠EBF+∠F=90°,∠ACF+∠F=90°
∴∠EBF=∠ACF.
在△ABD和△ACF中,
|
∴△ABD≌△ACF(ASA)
∴BD=CF
在△BCE和△BFE中,
|
∴△BCE≌△BFE(ASA)
∴CE=EF
∴BD=CF=2CE.
点评:本题主要考查了全等三角形的证明,能够想到延长CE、BA相交于点F,构造全等三角形是解决本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
用科学记数法表示为1.999×103的数是( )
| A、1999 |
| B、199.9 |
| C、0.001999 |
| D、19990 |
 根据输入的有理数,按图中程序计算,并把输出的结果填入表内.提示:要有适当的运算过程
根据输入的有理数,按图中程序计算,并把输出的结果填入表内.提示:要有适当的运算过程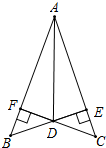 如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于 点D,DE=DF,连结AD.
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于 点D,DE=DF,连结AD.