题目内容
10.等腰三角形的周长为5(2+$\sqrt{3}$),顶角是底角的4倍,求各角与各边的长.分析 根据等腰三角形顶角是底角的4倍,可以求得各内角的度数,作辅助线AD⊥BC,找出三边之间的关系,再根据等腰三角形的周长为5(2+$\sqrt{3}$),可以求得各边的长,从而可以解答本题.
解答 解:∵腰三角形顶角是底角的4倍,
∴设该等腰三角形的底角为x,则顶角为4x.
∴x+x+4x=180°.
解得x=30°,
4x=120°.
如下图所示:AB=AC,∠B=∠C=30°,作AD⊥BC交BC于点D.
∵AD⊥BC,
∴∠ADB=90°.
∵AB=AC,∠B=∠C=30°,
∴BD=CD=$\frac{1}{2}BC$,BD=ABcos30°.
∵等腰三角形ABC的周长为5(2+$\sqrt{3}$),
∴AB+2ABcos30°+AC=5(2+$\sqrt{3}$).
解得,AB=AC=5,BC=5$\sqrt{3}$.
即该等腰三角形的各角分别为:30°,30°,120°,各边分别为:5,5,5$\sqrt{3}$.
点评 本题考查解直角三角形、等边三角形的性质,解题的关键是找出所求问题需要的条件,明确各个量之间的关系.

练习册系列答案
相关题目
 如图所示,在平面直角坐标系中,A、B两点分别是y轴、x轴上的两个动点,∠CAB=90°,AB=4,AC=3,当A、B两点在x、y轴的正半轴上运动时,OC的最大距离是$\frac{5+\sqrt{61}}{2}$.
如图所示,在平面直角坐标系中,A、B两点分别是y轴、x轴上的两个动点,∠CAB=90°,AB=4,AC=3,当A、B两点在x、y轴的正半轴上运动时,OC的最大距离是$\frac{5+\sqrt{61}}{2}$.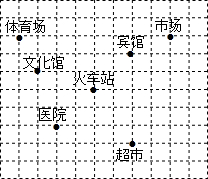 如图,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其它各地点的坐标.
如图,这是某城市部分简图,每个小正方形的边长为1个单位长度,已知火车站的坐标为(1,2),试建立平面直角坐标系,并分别写出其它各地点的坐标.