题目内容
如图,已知∠1=∠2, ∠3=∠4。试说明AC=AD成立的理由。 请同学们完成下列填空.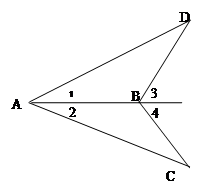
解:∵ ∠3=∠4( 已知 )
∴ ∠ABC=∠ABD( )
在△ABC和△ABD中,
 ∠1=∠2( 已知 ),
∠1=∠2( 已知 ), ( ),
∠ABC=∠ABD,
∴△ABC≌△DEF( ),
∴AC=AB( ).
解:∵ ∠3=∠4( 已知 )
∴ ∠ABC=∠ABD( 等角的补角相等 )
在△ABC和△ABD中,
 ∠1=∠2( 已知 ),
∠1=∠2( 已知 ),
AB =" AB" ( 公共边 ),
∠ABC=∠ABD,
∴△ABC≌△DEF( ASA ),
∴AC=AB(全等三角形的对应边相等)解析:
利用ASA,求得三角形全等,从而求解
∴ ∠ABC=∠ABD( 等角的补角相等 )
在△ABC和△ABD中,
 ∠1=∠2( 已知 ),
∠1=∠2( 已知 ), AB =" AB" ( 公共边 ),
∠ABC=∠ABD,
∴△ABC≌△DEF( ASA ),
∴AC=AB(全等三角形的对应边相等)解析:
利用ASA,求得三角形全等,从而求解

练习册系列答案
相关题目
 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 =2,∠ADC=30°
=2,∠ADC=30° 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=