题目内容
△ABC中，若AB=6，BC=8，∠B=120°，则△ABC的面积为
- A.
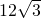
- B.12
- C.
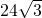
- D.
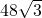
A
分析：作三角形的高AD，在直角△ABD中，利用三角函数即可求得AD的长，然后利用三角形的面积公式即可求解．
解答：
解：作AD⊥BC于点D．
∵∠B=120°，
∴∠ABD=180°-120°=60°，
在直角△ABD中，AD=AB•sin60°=6×
=3
，
在△ABC的面积是：
BC•AD=×8×3=12．
故选A．
点评：本题考查了三角形的面积公式以及三角函数，正确求得三角形的高是关键．
分析：作三角形的高AD，在直角△ABD中，利用三角函数即可求得AD的长，然后利用三角形的面积公式即可求解．
解答：
解：作AD⊥BC于点D．∵∠B=120°，
∴∠ABD=180°-120°=60°，
在直角△ABD中，AD=AB•sin60°=6×
=3，在△ABC的面积是：
BC•AD=×8×3=12．故选A．
点评：本题考查了三角形的面积公式以及三角函数，正确求得三角形的高是关键．
练习册系列答案
相关题目
21、如图，在△ABC中，若AB=AC，角平分线BD、CE相交于点O，OB与OC相等吗？请说明理由．
如图，在△ABC中，若AB=5，AC=2，∠BAC=120°．以BC为边作等边三角形BCD，把△ABD绕D点按顺时针方向旋转60°到△ECD的位置．