题目内容
.我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设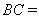
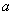 ,
,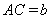 ,
,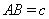 .
.
特例探索
(1)如图1,当∠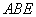 =45°,
=45°,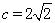 时,
时,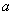 = ,
= ,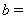 ;
;
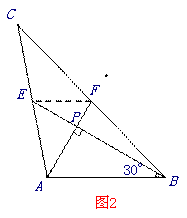
如图2,当∠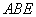 =30°,
=30°,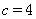 时,
时, 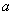 = ,
= ,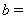 ;
;

归纳证明
(2)请你观察(1)中的计算结果,猜想 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
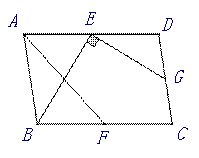
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD= 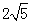 ,AB=3.
,AB=3.
求AF的长.
解析:(1)如图1,连接EF,则EF是△ABC的中位线,
∴EF=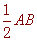 =
=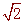 ,
,
∵∠ABE=45°,AE⊥EF ∴△ABP是等腰直角三角形,
∵EF∥AB ,∴△EFP也是等腰直角三角形,
∴AP=BP=2 ,EP=FP=1, ∴AE=BF= ,
,
∴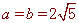 .
.
 如图2,连接EF,则EF是△ABC的中位线.
如图2,连接EF,则EF是△ABC的中位线.
∵∠ABE=30°,AE⊥BF,AB=4,
∴AP=2, BP=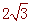 ,
,
∵EF
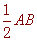 , ∴PE=
, ∴PE=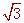 ,PF=1,
,PF=1,
∴AE=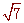 , BF=
, BF=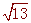
∴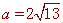 ,
, 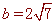 .
.
(2) 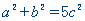
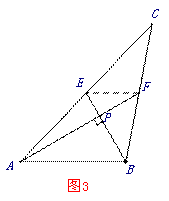 如图3,连接EF, 设AP=m ,BP=n.,则
如图3,连接EF, 设AP=m ,BP=n.,则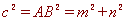
∵EF
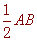 , ∴PE=
, ∴PE=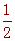 BP=
BP=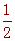 n , PF=
n , PF=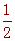 AP=
AP=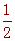 m,
m,
∴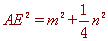 ,
, 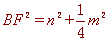 ,
,
∴ ,
,
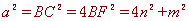
∴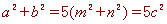
(3)
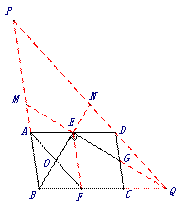
如上图,延长EG,BC交于点Q, 延长QD,BA交于点P,延长QE,BE分别交PB,PQ于点M,N,连接EF.
∵四边形ABCD是平行四边形,∴AD BC, AB
BC, AB CD,
CD,
∵E,G是分别是AD,CD的中点,∴△EDG≌△QCG≌△EAM, ∴CQ=DE= , DG=AM=1.5,∴BM=4.5.
, DG=AM=1.5,∴BM=4.5.
∵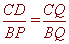 ,∴
,∴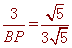 ,∴BP=9, ∴M是BP的中点;
,∴BP=9, ∴M是BP的中点;
∵AD FQ, ∴四边形ADQF是平行四边形,∴AF∥PQ,
FQ, ∴四边形ADQF是平行四边形,∴AF∥PQ,
∵E,F分别是AD,BC的中点,∴AE BF, ∴四边形ABFE是平行四边形,∴OA=OF,
BF, ∴四边形ABFE是平行四边形,∴OA=OF,
由AF∥PQ得:
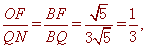
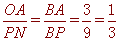 , ∴
, ∴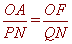 , ∴PN=QN, ∴N是PQ的中点;
, ∴PN=QN, ∴N是PQ的中点;
∴△BQP是“中垂三角形”, ∴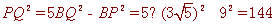 ,
,
∴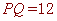 , ∴
, ∴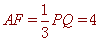

 ,3
,3
 角的直角三角板ABC的直角顶点A在直线DE上, 且BC//DE,则
角的直角三角板ABC的直角顶点A在直线DE上, 且BC//DE,则 等于( )
等于( ) (C)60
(C)60
 4}=4,按照这个规定,方程
4}=4,按照这个规定,方程 的解为( )
的解为( )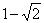 (B)
(B)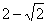 (C)
(C)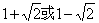 (D)
(D)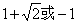
 6a²
6a² 排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 m.
排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为 m.