题目内容
(1)在Rt△ABC中,∠C=90°,c=5,且cos2A- cosA+1=0.求∠A的对边a;
cosA+1=0.求∠A的对边a;
(2)在Rt△ABC中,∠C=90°,∠A=60°,∠B、∠C的对边之和b+c=6.求∠A的对边a.
解:(1)∵cos2A- cosA+1=0
cosA+1=0
由求根公式得:cosA= =
=
∵cosA≤1,∴cosA= +1>1,舍去
+1>1,舍去
∴cosA= -1=
-1=
∵c=5
∴b=5 -5,a=
-5,a= =5
=5 ;
;
(2)∵cosA=cos60°= =
= ,b+c=6,
,b+c=6,
解得b=2,c=4,
∴a= =
=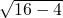 =
= =2
=2 .
.
分析:(1)根据求根公式求出cosA值后,再利用锐角三角函数的概念和勾股定理求a;
(2)根据锐角三角函数的概念和勾股定理求a.
点评:本题考查了解直角三角形的能力,第一小题中还用到了一元二次方程的求根公式.
 cosA+1=0
cosA+1=0由求根公式得:cosA=
 =
=
∵cosA≤1,∴cosA=
 +1>1,舍去
+1>1,舍去∴cosA=
 -1=
-1=
∵c=5
∴b=5
 -5,a=
-5,a= =5
=5 ;
;(2)∵cosA=cos60°=
 =
= ,b+c=6,
,b+c=6,解得b=2,c=4,
∴a=
 =
=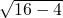 =
= =2
=2 .
.分析:(1)根据求根公式求出cosA值后,再利用锐角三角函数的概念和勾股定理求a;
(2)根据锐角三角函数的概念和勾股定理求a.
点评:本题考查了解直角三角形的能力,第一小题中还用到了一元二次方程的求根公式.

练习册系列答案
相关题目
 23、如图,在Rt△ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,求BD的长.
23、如图,在Rt△ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,求BD的长.