题目内容
 如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于
如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于
- A.2cosα
- B.2sinα
- C.

- D.

C
分析:连接CD和BE,并过C点作CF∥DE交BE于F,因为点C在线段AB上,AB、AC为直径,可证,CD∥BE,∠AEB=∠ADC=90°,故有CF=DE=2,∠CFB=∠EAB=α,根据三角函数关系,可得BC= .
.
解答: 解:连接CD、BE,过C点作CF∥AE交BE于点F,
解:连接CD、BE,过C点作CF∥AE交BE于点F,
点C在线段AB上,AB、AC为直径,
所以有DC⊥AE,BE⊥AE,
即得CD∥BE,且四边形DCFE为正方形,
即FC=DE=2,∠CFB=∠EAB=α,
在Rt△BCF中,BC=
故选C.
点评:本题主要考查了直径所对的圆周角为直角的知识,利用三角函数关系式求解直角三角形.
分析:连接CD和BE,并过C点作CF∥DE交BE于F,因为点C在线段AB上,AB、AC为直径,可证,CD∥BE,∠AEB=∠ADC=90°,故有CF=DE=2,∠CFB=∠EAB=α,根据三角函数关系,可得BC=
 .
.解答:
 解:连接CD、BE,过C点作CF∥AE交BE于点F,
解:连接CD、BE,过C点作CF∥AE交BE于点F,点C在线段AB上,AB、AC为直径,
所以有DC⊥AE,BE⊥AE,
即得CD∥BE,且四边形DCFE为正方形,
即FC=DE=2,∠CFB=∠EAB=α,
在Rt△BCF中,BC=

故选C.
点评:本题主要考查了直径所对的圆周角为直角的知识,利用三角函数关系式求解直角三角形.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目

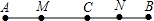
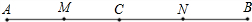
 (1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=18cm,BC=6cm,点M、N分别是AC、BC的中点,求MN的长; 如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=
如图,点M在线段AB上,MB=4cm,NB=9cm,且N是AM的中点,则AB=