题目内容
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,
(1)∠ABC=42°,∠A=60°,求∠BFC的度数;
(2)直接写出∠A与∠BFC的数量关系.
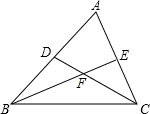
【考点】三角形内角和定理.
【分析】(1)根据角平分线的定义可得∠FBC=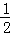 ∠ABC,∠FCB=
∠ABC,∠FCB=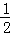 ∠ACB,再根据三角形内角和定理求出即可;
∠ACB,再根据三角形内角和定理求出即可;
(2)根据角平分线的定义可得∠FBC=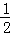 ∠ABC,∠FCB=
∠ABC,∠FCB=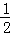 ∠ACB,然后表示出∠FBC+∠FCB,再根据三角形的内角和等于180°列式整理即可得证.
∠ACB,然后表示出∠FBC+∠FCB,再根据三角形的内角和等于180°列式整理即可得证.
【解答】解:(1)∵∠ABC=42°,∠A=60°,
∴∠ACB=78°,
∵∠ABC、∠ACB的平分线相交于点F,
∴∠FBC=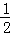 ∠ABC=21°,∠FCB=
∠ABC=21°,∠FCB=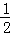 ∠ACB=39°,
∠ACB=39°,
∴∠BFC=180°﹣(∠FBC+∠FCB)=120°;
(2)∠BFC=90°+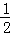 A,
A,
理由是:∵∠ABC与∠ACB的平分线相交于点F,
∴∠FBC=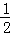 ∠ABC,∠FCB=
∠ABC,∠FCB=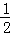 ∠ACB,
∠ACB,
∴∠FBC+∠FCB=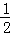 (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△FBC中,∠BFC=180°﹣(∠FBC+∠FCB)
=180°﹣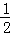 (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣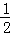 (180°﹣∠A)
(180°﹣∠A)
=90°+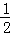 ∠A.
∠A.
【点评】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 B.
B. C.
C. D.
D.
 则它的周长是__________.
则它的周长是__________.
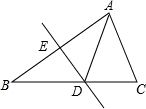
 D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.