题目内容
 在矩形ABCD中,BC=3,BG与对角线AC垂直且分别交AC、AD及射线CD于点E、F、G,设AB=x.
在矩形ABCD中,BC=3,BG与对角线AC垂直且分别交AC、AD及射线CD于点E、F、G,设AB=x.
(1)当点G与点D重合时,求x的值;
(2)当点F为AD中点时,求x的值及∠ECF的正弦值;
(3)是否存在x的值,使以点D为圆心、CD为半径的圆与BG相切?若存在,求出x的值;若不存在,请说明理由.
解:(1)当点G与点D重合时,点F也与点D重合,
∵矩形ABCD中,AC⊥BG,
∴四边形ABCD是正方形,
∵BC=3,
∴x=AB=BC=3;
(2)∵点F为AD中点,且AD=BC=3,
∴AF= AD=
AD= ,
,
∵矩形ABCD中,AD∥BC,
∴∠EAF=∠ECB,∠AFE=∠CBE,
∴△AEF∽△CEB,
∴ =
= =
=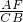 =
=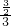 =
= ,
,
∴CE=2AE,BE=2FE,∴AC=3AE,BF=3FE,
∵矩形ABCD中,∠ABC=∠BAF=90°,
∴在Rt△ABC和Rt△BAF中,
分别由勾股定理得:AC2=AB2+BC2,BF2=AF2+AB2,
即(3AE)2=x2+32,
(3FE)2=( )2+x2,
)2+x2,
两式相加,得:9(AE2+FE2)=2x2+ ,
,
又∵AC⊥BG,
∴在Rt△ABE中,根据勾股定理得:AE2+FE2=AF2= ,
,
∴9× =2x2+
=2x2+ ,
,
解得:x=
 或x=-
或x=-
 (舍去),
(舍去),
故x=
 ;
;
∵F为AD的中点,由对称性(或△BAF≌△CDF)得到BF=CF,
∴在Rt△FEC中,sin∠ECF=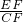 =
= =
= .
.
(3)存在,
理由:连接BD交AC于点O,过D作DH⊥BG于H.
则当DH=DC时,以点D为圆心、CD为半径的圆与BG相切.
∵在Rt△BHD和Rt△BCD中

∴Rt△BHD≌Rt△BCD(HL),
∴BH=BC,
∵AC⊥BG,DH⊥BG,
∴HD∥EO,
∴△BEO∽△BHD,
∴ =
= ,
,
∴ =
= ,
,
∴∠ACB=30°,
∴在Rt△ABC中,x=AB= BC=
BC= .
.
分析:(1)根据当点G与点D重合时,点F也与点D重合,进而利用正方形的性质得出x的值;
(2)首先得出△AEF∽△CEB,进而得出CE=2AE,BE=2FE,再利用勾股定理得出x的值,再利用sin∠ECF=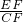 =
= 得出;
得出;
(3)首先根据当DH=DC时,以点D为圆心、CD为半径的圆与BG相切,先证明Rt△BHD≌Rt△BCD,得出BH=BC,进而得出△BEO∽△BHD,即可得出x的值.
点评:此题主要考查了圆的综合应用以及相似三角形的判定与性质和全等三角形的判定与性质以及切线的性质等知识,熟练掌握相关定理是解题关键.
∵矩形ABCD中,AC⊥BG,
∴四边形ABCD是正方形,
∵BC=3,
∴x=AB=BC=3;
(2)∵点F为AD中点,且AD=BC=3,
∴AF=
 AD=
AD= ,
,∵矩形ABCD中,AD∥BC,
∴∠EAF=∠ECB,∠AFE=∠CBE,
∴△AEF∽△CEB,
∴
 =
= =
=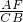 =
=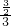 =
= ,
,∴CE=2AE,BE=2FE,∴AC=3AE,BF=3FE,
∵矩形ABCD中,∠ABC=∠BAF=90°,
∴在Rt△ABC和Rt△BAF中,
分别由勾股定理得:AC2=AB2+BC2,BF2=AF2+AB2,
即(3AE)2=x2+32,
(3FE)2=(
 )2+x2,
)2+x2,两式相加,得:9(AE2+FE2)=2x2+
 ,
,又∵AC⊥BG,
∴在Rt△ABE中,根据勾股定理得:AE2+FE2=AF2=
 ,
,∴9×
 =2x2+
=2x2+ ,
,解得:x=

 或x=-
或x=-
 (舍去),
(舍去),故x=

 ;
;∵F为AD的中点,由对称性(或△BAF≌△CDF)得到BF=CF,
∴在Rt△FEC中,sin∠ECF=
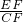 =
= =
= .
.
(3)存在,
理由:连接BD交AC于点O,过D作DH⊥BG于H.
则当DH=DC时,以点D为圆心、CD为半径的圆与BG相切.
∵在Rt△BHD和Rt△BCD中

∴Rt△BHD≌Rt△BCD(HL),
∴BH=BC,
∵AC⊥BG,DH⊥BG,
∴HD∥EO,
∴△BEO∽△BHD,
∴
 =
= ,
,∴
 =
= ,
,∴∠ACB=30°,
∴在Rt△ABC中,x=AB=
 BC=
BC= .
.分析:(1)根据当点G与点D重合时,点F也与点D重合,进而利用正方形的性质得出x的值;
(2)首先得出△AEF∽△CEB,进而得出CE=2AE,BE=2FE,再利用勾股定理得出x的值,再利用sin∠ECF=
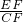 =
= 得出;
得出;(3)首先根据当DH=DC时,以点D为圆心、CD为半径的圆与BG相切,先证明Rt△BHD≌Rt△BCD,得出BH=BC,进而得出△BEO∽△BHD,即可得出x的值.
点评:此题主要考查了圆的综合应用以及相似三角形的判定与性质和全等三角形的判定与性质以及切线的性质等知识,熟练掌握相关定理是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( ) 如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围.
如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围. 如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF.
如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF. 在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE.
在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE. 如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.
如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.