题目内容
 如图,点P是线段AB、CD垂直平分线的交点,AD、BC交于点O,若PO平分∠BOD,求证:AD=BC.
如图,点P是线段AB、CD垂直平分线的交点,AD、BC交于点O,若PO平分∠BOD,求证:AD=BC.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:连接AP、CP.欲证明AD=BC,只需通过SAS推知△APD≌△BPC.
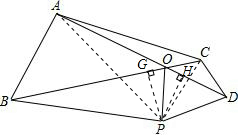
解答:证明:如图,连接AP、CP,过点P作PG⊥BC于G、PH⊥AD于H.
 ∵PO平分∠BOD,点P是线段AB、CD垂直平分线的交点,
∵PO平分∠BOD,点P是线段AB、CD垂直平分线的交点,
∴PG=PH,BP=AP,
在Rt△BPG与Rt△APH中,
,
∴Rt△BPG≌Rt△APH(HL),
同理,Rt△DPH≌Rt△CPG,
∴∠PBG=∠PAH,∠PDH=∠PCG,
在△PBC与△PAD中,
,
∴△PBC≌△PAD(ASA),
∴BC=AD,即AD=BC.
 ∵PO平分∠BOD,点P是线段AB、CD垂直平分线的交点,
∵PO平分∠BOD,点P是线段AB、CD垂直平分线的交点,∴PG=PH,BP=AP,
在Rt△BPG与Rt△APH中,
|
∴Rt△BPG≌Rt△APH(HL),
同理,Rt△DPH≌Rt△CPG,
∴∠PBG=∠PAH,∠PDH=∠PCG,
在△PBC与△PAD中,
|
∴△PBC≌△PAD(ASA),
∴BC=AD,即AD=BC.
点评:本题考查了全等三角形的判定与性质,在推知全等三角形的条件时,利用了线段垂直平分线的性质和角平分线的性质.

练习册系列答案
相关题目
直线AB上有一点M,直线AB外有一点N,过这四个点中的任意两点可确定直线( )
| A、5条 | B、4条 | C、3条 | D、2条 |
登山队员攀登珠穆朗玛峰,在海拔3000m时,气温为-20℃,已知每登高1000m,气温降低6℃,当海拔为5000m时,气温是( )℃.
| A、-50 | B、-42 |
| C、-40 | D、-32 |
下列说法正确的是( )
| A、一组对边相等,另一组对边平行的四边形是平行四边形 |
| B、四边相等的四边形是菱形 |
| C、对角线相等且垂直的四边形是正方形 |
| D、对角线互相垂直的平行四边形是矩形 |
 如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.

 在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.