题目内容
如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB= ,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
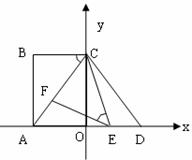
(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.
【解析】(1)∵四边形ABCO为矩形,∴AO=BC,AB=OC,∠B=90°,∴在Rt△ABC中, AB=4,BC=3,由勾股定理,得AC=5.∴AO=3.∵点D与点A关于y轴对称,∴AO=DO.∴DO=3,
∴D(3,0);
(2)点D与点A关于y轴对称,∴∠CDE=∠CAO,∴AC=CD=5.∵∠CEF=∠ACB,∠ACB=∠CAO,∴∠CDE=∠CEF,∵∠AFE=∠ACE+∠CEF,∠DEC=∠ACE+∠CAO,∴∠AFE=∠DEC.
∵在△AEF与△DCE中, ,∴△AEF∽△DCE(AA).
,∴△AEF∽△DCE(AA).
(3)当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,∵△AEF∽△DCE,∴△AEF≌△DCE,∴AE=CD=5,∴OE=AE-OA=5-3=2,
∴E(2,0);
②当EF=FC时,∵∠FCE=∠FEC=∠ACB=∠CAE ,∴AE=CE
设E(a ,0),∴OE2+OC2=CE2=AE2=(OA+OE)2 即:
解得a= 此时,点E的坐标为(
此时,点E的坐标为( ,0)
,0)
③当CE=CF时,E与D重合与题目矛盾.
综上所述,当△EFC为等腰三角形时,点E的坐标为(2,0)或( ,0)
,0)

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
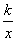 ,则k=
,则k= 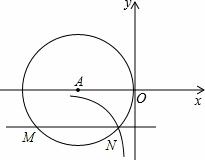

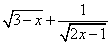 有意义,则x应满足( ).
有意义,则x应满足( ).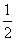 ≤x≤3 B.x≤3且x≠
≤x≤3 B.x≤3且x≠
