题目内容
正方形 边长为4,
边长为4, 、
、 分别是
分别是 、
、 上的两个动点,当
上的两个动点,当 点在
点在 上运动时,保持
上运动时,保持 和
和 垂直,设MB=x
垂直,设MB=x
(1)证明:
 ;
;(2)当
 点运动到什么位置时
点运动到什么位置时 ,
,求此时
 的值.
的值.
(1)证明过程见解析,(2)M运动到BC中点时相似,x=2解析:
(1)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
又∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMC=90°,
而∠AMB+∠BAM=90°,
∴∠BAM=∠NMC,
∴Rt△ABM∽Rt△MCN,
(2)M运动到BC中点时相似
∵△ABM∽△AMN,
∴AB:BM=AM:MN,又MB=x,
AM= ,
,
MN= =
= 
 :
: =
=
∴4:x= :
: ,
,
(4-x)2(16+x2)=x2(16+x2),
16-8x=0,
解得x=2.即M运动到BC中点时相似
(1)证明:∵四边形ABCD为正方形,
∴∠B=∠C=90°,
又∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMC=90°,
而∠AMB+∠BAM=90°,
∴∠BAM=∠NMC,
∴Rt△ABM∽Rt△MCN,
(2)M运动到BC中点时相似
∵△ABM∽△AMN,
∴AB:BM=AM:MN,又MB=x,
AM=
 ,
,MN=
 =
= 
 :
: =
=
∴4:x=
 :
: ,
,(4-x)2(16+x2)=x2(16+x2),
16-8x=0,
解得x=2.即M运动到BC中点时相似

练习册系列答案
相关题目

 边长为4,
边长为4, 、
、 分别是
分别是 、
、 上的两个动点,当
上的两个动点,当 和
和 垂直,
垂直,
 ;
; ,梯形
,梯形 的面积为
的面积为 ,求
,求 之间的函数关系式;
之间的函数关系式; 边长为4,
边长为4, 、
、 分别是
分别是 、
、 上的两个动点,当
上的两个动点,当 和
和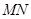 垂直,
垂直,
 ;
; ,梯形
,梯形 的面积为
的面积为 ,求
,求 之间的函数关系式;
之间的函数关系式; 边长为4,
边长为4, 、
、 分别是
分别是 、
、 上的两个动点,当
上的两个动点,当 和
和 垂直,设MB=x
垂直,设MB=x
 ;
; ,
, 的值.
的值. 边长为4,
边长为4, 、
、 分别是
分别是 、
、 上的两个动点,当
上的两个动点,当 和
和 垂直,
垂直,
 ;
; ,梯形
,梯形 的面积为
的面积为 ,求
,求 之间的函数关系式;
之间的函数关系式;