题目内容
如图1,在直角梯形ABCD中,AD∥BC,顶点D,C分别在AM,BN上运动(点D不与A重合,点C不与B重合),E是AB上的动点(点E不与A,B重合),在运动过程中始终保持DE⊥CE,且AD+DE=AB=a.(1)求证:△ADE∽△BEC;
(2)当点E为AB边的中点时(如图2),求证:①AD+BC=CD;②DE,CE分别平分∠ADC,∠BCD;
(3)设AE=m,请探究:△BEC的周长是否与m值有关,若有关请用含m的代数式表示△BEC的周长;若无关请说明理由.

分析:(1)∠A=∠D=90°,然后利用∠DEC=90°得到∠AED=∠ECB,这样就可以证明△ADE∽△BEC;
(2)过点E作梯形两底的平行线交腰CD于F,则F是CD的中点,然后利用梯形的中位线就可以证明①和②;
(3)主要利用(1)中的相似三角形带来的比例线段和勾股定理解题.
(2)过点E作梯形两底的平行线交腰CD于F,则F是CD的中点,然后利用梯形的中位线就可以证明①和②;
(3)主要利用(1)中的相似三角形带来的比例线段和勾股定理解题.
解答:(1)证明:∵梯形ABCD是直角梯形
∴∠A=∠B=90°
又∵∠DEC=90°
∴∠AED+∠BEC=90°
∵∠BEC+∠BCE=90°
∴∠AED=∠BCE
∴△ADE∽△BEC
(2)证明:过点E作EF∥AD,交CD于F,则EF既是梯形ABCD的中位线,又是Rt△DEC斜边上的中线.
∵AD+BC=2EF,CD=2EF
∴AD+BC=CD
∵FD=FE=
CD
∴∠FDE=∠FED
∵EF∥AD
∴∠ADE=∠FED
∴∠FDE=∠ADE,即DE平分∠ADC
同理可证:CE平分∠BCD
(3)解:设AD=x,由已知AD+DE=AB=a得DE=a-x,又AE=m
在Rt△AED中,由勾股定理得:x2+m2=(a-x)2,化简整理得:a2-m2=2ax①
在△EBC中,由AE=m,AB=a,得BE=a-m
因为△ADE∽△BEC,所以
=
=
,
即:
=
=
,
解得:BC=
,EC=
所以△BEC的周长=BE+BC+EC=(a-m)+
+
=(a-m)(1+
+
)=(a-m)•
=
②
把①式代入②,得△BEC的周长=BE+BC+EC=
=2a
所以△BEC的周长与m无关.
∴∠A=∠B=90°
又∵∠DEC=90°
∴∠AED+∠BEC=90°
∵∠BEC+∠BCE=90°
∴∠AED=∠BCE
∴△ADE∽△BEC
(2)证明:过点E作EF∥AD,交CD于F,则EF既是梯形ABCD的中位线,又是Rt△DEC斜边上的中线.
∵AD+BC=2EF,CD=2EF

∴AD+BC=CD
∵FD=FE=
| 1 |
| 2 |
∴∠FDE=∠FED
∵EF∥AD
∴∠ADE=∠FED
∴∠FDE=∠ADE,即DE平分∠ADC
同理可证:CE平分∠BCD
(3)解:设AD=x,由已知AD+DE=AB=a得DE=a-x,又AE=m
在Rt△AED中,由勾股定理得:x2+m2=(a-x)2,化简整理得:a2-m2=2ax①
在△EBC中,由AE=m,AB=a,得BE=a-m
因为△ADE∽△BEC,所以
| AD |
| BE |
| AE |
| BC |
| DE |
| EC |
即:
| x |
| a-m |
| m |
| BC |
| a-x |
| EC |
解得:BC=
| (a-m)m |
| x |
| (a-m)(a-x) |
| x |
所以△BEC的周长=BE+BC+EC=(a-m)+
| (a-m)m |
| x |
| (a-m)(a-x) |
| x |
=(a-m)(1+
| m |
| x |
| a-x |
| x |
| a+m |
| x |
=
| a2-m2 |
| x |
把①式代入②,得△BEC的周长=BE+BC+EC=
| 2ax |
| x |
所以△BEC的周长与m无关.
点评:此题主要考查了梯形的中位线的性质,相似三角形的判定与性质,勾股定理及直角三角形的性质等知识点的综合运用.

练习册系列答案
相关题目
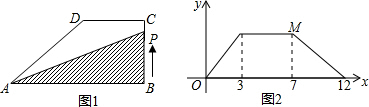
 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )| A、3 | B、4 | C、5 | D、6 |