题目内容
如图,直线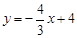 与
与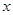 轴、
轴、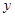 轴分别交于
轴分别交于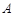 、
、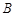 两点,△
两点,△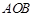 绕点
绕点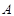 顺时针旋转90后得到△
顺时针旋转90后得到△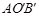 ,则点
,则点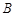 的对应点
的对应点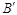 坐标为
坐标为

A.(3,4) B.(7,4)
C.(7,3) D.(3,7)
【答案】
C
【解析】
试题分析:∵y=- +4 与x轴 y轴相交 易得A(3,0)
B(0,4) ∴AO="3" BO="4" ∵△AOB绕点A顺时针旋转90后得到,△AOB≌△AO′B′
∴∠O′AB′="∠OAB" 又∵∠BAB′="90"
∴∠B′AX=∠BAO”∴∠OAO′=90∴∠B′=∠B′AX ∴OA∥O′B′ ∴B′(7,3)
+4 与x轴 y轴相交 易得A(3,0)
B(0,4) ∴AO="3" BO="4" ∵△AOB绕点A顺时针旋转90后得到,△AOB≌△AO′B′
∴∠O′AB′="∠OAB" 又∵∠BAB′="90"
∴∠B′AX=∠BAO”∴∠OAO′=90∴∠B′=∠B′AX ∴OA∥O′B′ ∴B′(7,3)
考点:一次函数的知识,图形旋转后的性质,三角形全等及等量代换,坐标点的定义。
点评:掌握一次函数的图像与坐标轴的交点求法,旋转后的图形大小形状不变,同角的余角相等,坐标点的简单求法。有点难度,但不大。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 与
与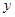 轴的交点坐标为A(0,1),与
轴的交点坐标为A(0,1),与 轴的交点坐标为B(-3,0);P、Q分别是
轴的交点坐标为B(-3,0);P、Q分别是
 S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;
S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;
 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从
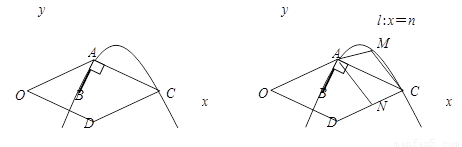 (3)如图2,设垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
(3)如图2,设垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.