题目内容
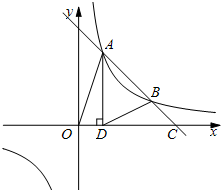 如图,直线y=ax+b与双曲线
如图,直线y=ax+b与双曲线 交于点A、B,与x轴交于点C,AD⊥x轴于点D,且cos∠AOC=
交于点A、B,与x轴交于点C,AD⊥x轴于点D,且cos∠AOC= ,AD=6,S△ABD=2S△AOD.
,AD=6,S△ABD=2S△AOD.
(1)求双曲线与直线的解析式;
(2)连接OB,求△AOB的面积.
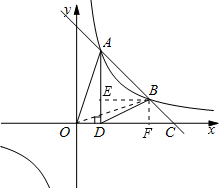 解:(1)在Rt△AOD中,cos∠AOC=
解:(1)在Rt△AOD中,cos∠AOC= ,
,设OD=m,则OA=
 m,又AD=6,
m,又AD=6,根据勾股定理得:OA2=OD2+AD2,即(
 m)2=m2+62,
m)2=m2+62,解得:m=2,
∴A(2,6),
将A的坐标代入反比例解析式得:6=
 ,
,解得:k=12,
则反比例解析式为y=
 ;
;过B作BE⊥AD,交AD于点E,
设B的横坐标为n,则BE=n-2,
∴S△ABD=
 ×6×(n-2),S△AOD=
×6×(n-2),S△AOD= ×2×6=6,且S△ABD=2S△AOD,
×2×6=6,且S△ABD=2S△AOD,∴
 ×6×(n-2)=12,
×6×(n-2)=12,解得:n=6,
将x=6代入反比例解析式得:y=2,
∴B坐标为(6,2),
将A和B坐标代入y=ax+b得:
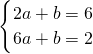 ,
,解得:
 ,
,则直线AB解析式为y=-x+8;
(2)过B作BF⊥y轴,交y轴于点F,
∵A(2,6),B(6,2),
∴AD=6,OD=2,BF=2,OF=6,DF=OF-OD=6-2=4,
则S△AOB=S△AOD+S梯形ABFD-S△BOF
=
 AD•OD+
AD•OD+ (BF+AD)•DF-
(BF+AD)•DF- BF•OF
BF•OF=
 ×2×6+
×2×6+ ×(2+6)×4-
×(2+6)×4- ×2×6
×2×6=16.
分析:(1)在Rt△AOD中,由cos∠AOC的值,利用锐角三角函数定义,设OD=m,则有OA=
 m,再由AD的长,利用勾股定理列出关于m的方程,求出方程的解得到m的值,确定出A的坐标,将A的坐标代入反比例解析式中求出k的值,确定出反比例解析式,过B作BE垂直于AD,设B横坐标为n,由OD的长为2,用n-2表示出BE,进而由AD为底,BE为高,表示出△ABD的面积,再求出△AOD的面积,根据△ABD的面积等于2△AOD的面积列出关于n的方程,求出方程的解得到n的值,即为B的横坐标,将B的横坐标代入反比例解析式中求出B的纵坐标,确定出B的坐标,将A和B两点坐标代入直线y=ax+b中,得到关于a与b的方程组,求出方程组的解得到a与b的值,即可确定出一次函数解析式;
m,再由AD的长,利用勾股定理列出关于m的方程,求出方程的解得到m的值,确定出A的坐标,将A的坐标代入反比例解析式中求出k的值,确定出反比例解析式,过B作BE垂直于AD,设B横坐标为n,由OD的长为2,用n-2表示出BE,进而由AD为底,BE为高,表示出△ABD的面积,再求出△AOD的面积,根据△ABD的面积等于2△AOD的面积列出关于n的方程,求出方程的解得到n的值,即为B的横坐标,将B的横坐标代入反比例解析式中求出B的纵坐标,确定出B的坐标,将A和B两点坐标代入直线y=ax+b中,得到关于a与b的方程组,求出方程组的解得到a与b的值,即可确定出一次函数解析式;(2)连接OB,过B作BF垂直于x轴,由A和B的坐标求出AD、OD、BF、OF的长,由△AOB的面积=△AOD的面积+梯形ABFD的面积-△OBF的面积,求出即可.
点评:此题属于反比例函数综合题,涉及的知识有:锐角三角函数定义,勾股定理,坐标与图形性质,以及待定系数法求函数解析式,待定系数法是数学中常用的解题方法,学生做题要灵活运用.

练习册系列答案
相关题目
 11、如图,直线y=ax+b经过点(-4,0),则不等式ax+b≥0的解集为
11、如图,直线y=ax+b经过点(-4,0),则不等式ax+b≥0的解集为 >0)相交于点P,PC⊥x轴于点C,点A的坐标为(-4,0),点B的坐标为(0,2),PC=3.
>0)相交于点P,PC⊥x轴于点C,点A的坐标为(-4,0),点B的坐标为(0,2),PC=3. (2013•大连一模)如图.直线y=ax+b与双曲线
(2013•大连一模)如图.直线y=ax+b与双曲线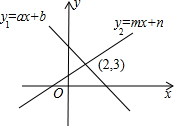 如图,直线y1=ax+b与直线y2=mx+n相交于点(2,3),则不等式ax+b>mx+n的解是( )
如图,直线y1=ax+b与直线y2=mx+n相交于点(2,3),则不等式ax+b>mx+n的解是( )