题目内容
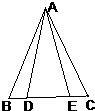 33、已知:如图,AB=AC,AD=AE,B、D、E、C在同一直线上,试判断BD与EC的大小关系,并说明理由.
33、已知:如图,AB=AC,AD=AE,B、D、E、C在同一直线上,试判断BD与EC的大小关系,并说明理由.分析:过点A作AM⊥BC于M,再利用等腰三角形三线合一的性质求得BM=CM,DM=EM,从而得出BM-DM=CM-EM,即BD=EC.
解答: 解:BD与EC相等.
解:BD与EC相等.
理由:过点A作AM⊥BC于M
∵B、D、E、C在同一直线上(已知)
∴AM⊥DE
又∵AB=AC,AD=AE(已知)
∴BM=CM,DM=EM(等腰三角形三线合-)
∴BM-DM=CM-EM即BD=EC.
 解:BD与EC相等.
解:BD与EC相等.理由:过点A作AM⊥BC于M
∵B、D、E、C在同一直线上(已知)
∴AM⊥DE
又∵AB=AC,AD=AE(已知)
∴BM=CM,DM=EM(等腰三角形三线合-)
∴BM-DM=CM-EM即BD=EC.
点评:主要考查了等腰三角形“三线合一“的性质;利用了等量减等量差相等时解答本题的关键.

练习册系列答案
相关题目
 8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( )
8、已知:如图,AB、AC分别切⊙O于B、C,D是⊙O上一点,∠D=40°,则∠A的度数等于( ) 已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.
已知:如图,AB,CD相交于点O,且OA•OD=OB•OC,求证:AC∥DB.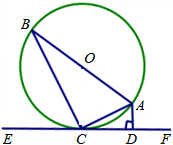 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
 29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD.
29、已知,如图,AB∥CD,∠EAB+∠FDC=180°.求证:AE∥FD. 已知:如图,AB=AC,DB=DC,求证:∠B=∠C.
已知:如图,AB=AC,DB=DC,求证:∠B=∠C.