题目内容
 如图,弦AB垂直于⊙O的直径CD,OA=5,AB=6,则BC=( )
如图,弦AB垂直于⊙O的直径CD,OA=5,AB=6,则BC=( )分析:根据垂径定理求出BM=AM=3,根据勾股定理求出OM,求出MC,根据勾股定理求出BC即可.
解答:解: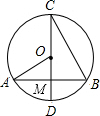
∵CD⊥AB,CD过O,AB=6,
∴AM=BM=3,
在Rt△OAM中,OA=5,AM=3,由勾股定理得:OM=4,
即CM=4+5=9,
在Rt△CMB中,CM=9,BM=3,由勾股定理得:BC=
=3
,
故选A.

∵CD⊥AB,CD过O,AB=6,
∴AM=BM=3,
在Rt△OAM中,OA=5,AM=3,由勾股定理得:OM=4,
即CM=4+5=9,
在Rt△CMB中,CM=9,BM=3,由勾股定理得:BC=
| 92+32 |
| 10 |
故选A.
点评:本题考查了垂径定理,勾股定理的应用,关键是求出CM和BM的长.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=
如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=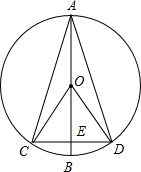 如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则
如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,则
 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=
如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD= 如图,弦AB垂直于⊙O的直径CD,OA=5,AB=6,则BC=
如图,弦AB垂直于⊙O的直径CD,OA=5,AB=6,则BC=