Question

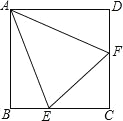
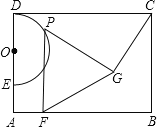
【题目】如图，E是矩形ABCD边AD上一点，以DE为直径向矩形内部作半圆O，AB=4，OD=2，点G在矩形内部，且∠GCB=30°，GC=2，过半圆弧（含点D，E）上动点P作PF⊥AB于点F．当△PFG是等边三角形时，PF的长是___．

Answer 1

【答案】4或6

【解析】

分两种情况：①作辅助线，构建直角三角形和等边三角形，先根据直角三角形30°的性质求GN的长，再证明D、P、G在一直线上，得△ODP是等边三角形，则PQ=，由此求出等边三角形PFG的高线GH的长，最后利用特殊的三角函数值求出边长．

②同理可得结论．

分两种情况：

①当P在正方形内部时，如图1，过G作GH⊥PF于H，交AD于M，BC于N，

∵△PFG是等边三角形，

∴∠PGH=∠PGF=×60°=30°，

Rt△CGN中，∵∠GCB=30°，CG=2，

∴GN=CG=，

∠CGN=60°，

∴∠CGP=180°-30°-60°=90°，

延长GP交直线CD于D′，

∵四边形ABCD是矩形，

∴∠BCD=90°，

∴∠DCG=60°，

∴∠CD′G=30°，

∴D′C=2CG=4，

∵CD=AB=4，

∴D与D′重合，

∴∠ADG=60°，

连接OP，过P作PQ⊥AD于Q，

∵OD=OP=2，

∴△ODP是等边三角形，

∴PQ=，

∴GH=4--=2，

Rt△PHG中，cos30°=，

∴PG=，

∴PF=PG=4，

②当P与D重合，则F与A重合，如图2，

过G作MN⊥BC，交AD于M，交BC于N，

若△PFG是等边三角形时，同理得：GN=，∠DGM=30°，

则MG=3，

∴DG=6，DM=3，

∴AD=6，

即PF=6，

综上所述，PF为4或6，

故答案为：4或6．