ЬтФПФкШн
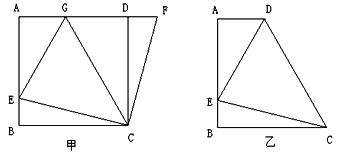
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпC1ЃКy=ax2Љ2ax+cЃЈaЃМ0ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЎвбжЊЕуAЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЕуOЮЊзјБъдЕуЃЌOC=3OAЃЌХзЮяЯпC1ЕФЖЅЕуЮЊGЃЎ

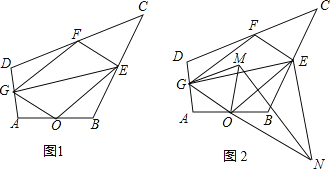
ЃЈ1ЃЉЧѓГіХзЮяЯпC1ЕФНтЮіЪНЃЌВЂаДГіЕуGЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌНЋХзЮяЯпC1ЯђЯТЦНвЦkЃЈkЃО0ЃЉИіЕЅЮЛЃЌЕУЕНХзЮяЯпC2ЃЌЩшC2гыxжсЕФНЛЕуЮЊAЁфЁЂBЁфЃЌЖЅЕуЮЊGЁфЃЌЕБЁїAЁфBЁфGЁфЪЧЕШБпШ§НЧаЮЪБЃЌЧѓkЕФжЕЃК
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМ3ЃЌЩшЕуMЮЊxжсе§АыжсЩЯвЛЖЏЕуЃЌЙ§ЕуMзїxжсЕФДЙЯпЗжБ№НЛХзЮяЯпC1ЁЂC2гкPЁЂQСНЕуЃЌЪдЬНОПдкжБЯпy=Љ1ЩЯЪЧЗёДцдкЕуNЃЌЪЙЕУвдPЁЂQЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOQШЋЕШЃЌШєДцдкЃЌжБНгаДГіЕуMЃЌNЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпC1ЕФНтЮіЪНЮЊy=Љx2+2x+3ЃЌЕуGЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЛЃЈ2ЃЉk=1ЃЛЃЈ3ЃЉM1ЃЈ![]() ЃЌ0ЃЉЁЂN1ЃЈ
ЃЌ0ЃЉЁЂN1ЃЈ![]() ЃЌЉ1ЃЉЃЛM2ЃЈ
ЃЌЉ1ЃЉЃЛM2ЃЈ![]() ЃЌ0ЃЉЁЂN2ЃЈ1ЃЌЉ1ЃЉЃЛM3ЃЈ4ЃЌ0ЃЉЁЂN3ЃЈ10ЃЌЉ1ЃЉЃЛM4ЃЈ4ЃЌ0ЃЉЁЂN4ЃЈЉ2ЃЌЉ1ЃЉЃЎ
ЃЌ0ЃЉЁЂN2ЃЈ1ЃЌЉ1ЃЉЃЛM3ЃЈ4ЃЌ0ЃЉЁЂN3ЃЈ10ЃЌЉ1ЃЉЃЛM4ЃЈ4ЃЌ0ЃЉЁЂN4ЃЈЉ2ЃЌЉ1ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЕуAЕФзјБъМАOC=3OAЕУЕуCзјБъЃЌНЋAЁЂCзјБъДњШыНтЮіЪНЧѓНтПЩЕУЃЛ
ЃЈ2ЃЉЩшХзЮяЯпC2ЕФНтЮіЪНЮЊy=Љx2+2x+3ЉkЃЌМДy=ЉЃЈxЉ1ЃЉ2+4ЉkЃЌЁфзїGЁфDЁЭxжсгкЕуDЃЌЩшBDЁф=mЃЌгЩЕШБпШ§НЧаЮаджЪжЊЕуBЁфЕФзјБъЮЊЃЈm+1ЃЌ0ЃЉЃЌЕуGЁфЕФзјБъЮЊЃЈ1ЃЌ![]() mЃЉЃЌДњШыЫљЩшНтЮіЪНЧѓНтПЩЕУЃЛ
mЃЉЃЌДњШыЫљЩшНтЮіЪНЧѓНтПЩЕУЃЛ
ЃЈ3ЃЉЩшMЃЈxЃЌ0ЃЉЃЌдђPЃЈxЃЌЉx2+2x+3ЃЉЁЂQЃЈxЃЌЉx2+2x+2ЃЉЃЌИљОнPQ=OA=1ЧвЁЯAOQЁЂЁЯPQNОљЮЊЖлНЧжЊЁїAOQЁеЁїPQNЃЌбгГЄPQНЛжБЯпy=Љ1гкЕуHЃЌжЄЁїOQMЁеЁїQNHЃЌИљОнЖдгІБпЯрЕШНЈСЂЙигкxЕФЗНГЬЃЌНтжЎЧѓЕУxЕФжЕДгЖјНјвЛВНЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁпЕуAЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌ
ЁрOA=1ЃЌ
ЁрOC=3OAЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
НЋAЁЂCзјБъДњШыy=ax2Љ2ax+cЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпC1ЕФНтЮіЪНЮЊy=Љx2+2x+3=ЉЃЈxЉ1ЃЉ2+4ЃЌ
ЫљвдЕуGЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉЩшХзЮяЯпC2ЕФНтЮіЪНЮЊy=Љx2+2x+3ЉkЃЌМДy=ЉЃЈxЉ1ЃЉ2+4ЉkЃЌ
Й§ЕуGЁфзїGЁфDЁЭxжсгкЕуDЃЌЩшBDЁф=mЃЌ

ЁпЁїAЁфBЁфGЁфЮЊЕШБпШ§НЧаЮЃЌ
ЁрGЁфD=![]() BЁфD=
BЁфD=![]() mЃЌ
mЃЌ
дђЕуBЁфЕФзјБъЮЊЃЈm+1ЃЌ0ЃЉЃЌЕуGЁфЕФзјБъЮЊЃЈ1ЃЌ![]() mЃЉЃЌ
mЃЉЃЌ
НЋЕуBЁфЁЂGЁфЕФзјБъДњШыy=ЉЃЈxЉ1ЃЉ2+4ЉkЃЌЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЈЩсЃЉЃЌ
ЃЈЩсЃЉЃЌ ЃЌ
ЃЌ
Ёрk=1ЃЛ
ЃЈ3ЃЉЩшMЃЈxЃЌ0ЃЉЃЌдђPЃЈxЃЌЉx2+2x+3ЃЉЁЂQЃЈxЃЌЉx2+2x+2ЃЉЃЌ
ЁрPQ=OA=1ЃЌ
ЁпЁЯAOQЁЂЁЯPQNОљЮЊЖлНЧЃЌ
ЁрЁїAOQЁеЁїPQNЃЌ
ШчЭМ2ЃЌбгГЄPQНЛжБЯпy=Љ1гкЕуHЃЌ

дђЁЯQHN=ЁЯOMQ=90ЁуЃЌ
гжЁпЁїAOQЁеЁїPQNЃЌ
ЁрOQ=QNЃЌЁЯAOQ=ЁЯPQNЃЌ
ЁрЁЯMOQ=ЁЯHQNЃЌ
ЁрЁїOQMЁеЁїQNHЃЈAASЃЉЃЌ
ЁрOM=QHЃЌМДx=Љx2+2x+2+1ЃЌ
НтЕУЃКx=![]() ЃЈИКжЕЩсШЅЃЉЃЌ
ЃЈИКжЕЩсШЅЃЉЃЌ
ЕБx=![]() ЪБЃЌHN=QM=Љx2+2x+2=
ЪБЃЌHN=QM=Љx2+2x+2=![]() ЃЌЕуMЃЈ
ЃЌЕуMЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрЕуNзјБъЮЊЃЈ![]() +
+![]() ЃЌЉ1ЃЉЃЌМДЃЈ
ЃЌЉ1ЃЉЃЌМДЃЈ![]() ЃЌЉ1ЃЉЃЛ
ЃЌЉ1ЃЉЃЛ
ЛђЃЈ![]() Љ
Љ![]() ЃЌЉ1ЃЉЃЌМДЃЈ1ЃЌЉ1ЃЉЃЛ
ЃЌЉ1ЃЉЃЌМДЃЈ1ЃЌЉ1ЃЉЃЛ
ШчЭМ3ЃЌ

ЭЌРэПЩЕУЁїOQMЁеЁїPNHЃЌ
ЁрOM=PHЃЌМДx=ЉЃЈЉx2+2x+2ЃЉЉ1ЃЌ
НтЕУЃКx=Љ1ЃЈЩсЃЉЛђx=4ЃЌ
ЕБx=4ЪБЃЌЕуMЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌHN=QM=ЉЃЈЉx2+2x+2ЃЉ=6ЃЌ
ЁрЕуNЕФзјБъЮЊЃЈ4+6ЃЌЉ1ЃЉМДЃЈ10ЃЌЉ1ЃЉЃЌЛђЃЈ4Љ6ЃЌЉ1ЃЉМДЃЈЉ2ЃЌЉ1ЃЉЃЛ
злЩЯЕуM1ЃЈ![]() ЃЌ0ЃЉЁЂN1ЃЈ
ЃЌ0ЃЉЁЂN1ЃЈ![]() ЃЌЉ1ЃЉЃЛM2ЃЈ
ЃЌЉ1ЃЉЃЛM2ЃЈ![]() ЃЌ0ЃЉЁЂN2ЃЈ1ЃЌЉ1ЃЉЃЛM3ЃЈ4ЃЌ0ЃЉЁЂN3ЃЈ10ЃЌЉ1ЃЉЃЛM4ЃЈ4ЃЌ0ЃЉЁЂN4ЃЈЉ2ЃЌЉ1ЃЉЃЎ
ЃЌ0ЃЉЁЂN2ЃЈ1ЃЌЉ1ЃЉЃЛM3ЃЈ4ЃЌ0ЃЉЁЂN3ЃЈ10ЃЌЉ1ЃЉЃЛM4ЃЈ4ЃЌ0ЃЉЁЂN4ЃЈЉ2ЃЌЉ1ЃЉЃЎ

 ГѕжаЪюЦкЯЮНгЯЕСаД№АИ
ГѕжаЪюЦкЯЮНгЯЕСаД№АИ