题目内容
如图，⊙O的直径CD⊥AB于点M，MD=2，AB=8，则CD长为
- A.5
- B.8
- C.10
- D.
C
分析：首先根据垂径定理得AM的值，再在直角△AOM中，根据勾股定理得半径，从而求出直径．
解答：
解：连接OA；
设圆的半径是r
首先根据垂径定理得AM=4，
再根据勾股定理得：
r2=（r-2）2+16，
r=5，
则直径CD=10；
故选C．
点评：此题综合运用了垂径定理和勾股定理．
分析：首先根据垂径定理得AM的值，再在直角△AOM中，根据勾股定理得半径，从而求出直径．
解答：
解：连接OA；设圆的半径是r
首先根据垂径定理得AM=4，
再根据勾股定理得：
r2=（r-2）2+16，
r=5，
则直径CD=10；
故选C．
点评：此题综合运用了垂径定理和勾股定理．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
如图，⊙O的直径CD过弦EF的中点G，∠EOD=40°，则∠DCF等于（ ）| A、80° | B、50° | C、40° | D、20° |
如图，⊙O的直径CD过弦EF的中点G，∠OEF=34°，则∠DCF的度数是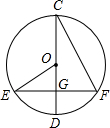
如图，⊙O的直径CD过弦EF的中点G，∠EOG=60°，则∠DCF的度数为
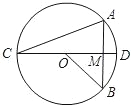如图，⊙O的直径CD过弦AB的中点M，∠ACD=28°，则∠B=