Question

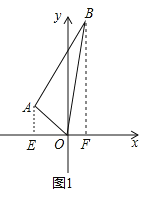
【题目】如图在平面直角坐标系中，A.B两点的坐标分别为（﹣2，2），（1，8），

（1）求△ABO的面积．

（2）若y轴上有一点M，且△MAB的面积为10．求M点的坐标．

（3）如图，把直线AB以每秒2个单位的速度向右平移，运动t秒钟后，直线AB过点F（0，﹣2），此时A点的坐标为　 　，B点的坐标为　 　，过点A作AE⊥y轴于点E，过点B作BD⊥y轴于点D，请根据S△FBD=S△FAE+S梯形ABDE，求出满足条件的运动时间t的值．

Answer 1

【答案】（1）9；（2）或；（3）

【解析】

（1）过作轴于，过作轴于，根据、两点的坐标分别为，，得到，，，于是得到结论；

（2）设直线的解析式为，于是得到直线的解析式为，解方程得到，根据三角形的面积列方程即可得到结论；

（3）设平移后的直线的解析式为：，把代入求得平移后的直线的解析式为：；根据图形的面积的计算方法即可得到结论.

（1）过作轴于，过作轴于，

、两点的坐标分别为，，

，，，

；

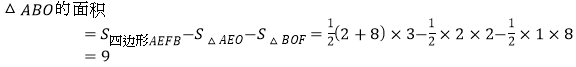（2）设直线的解析式为，

，

，

直线的解析式为，

直线与轴的交点坐标为，

设，

，

解得：或，

或；

（3）设平移后的直线的解析式为：，

把代入：得，

平移后的直线的解析式为：，

当时，；当时，，

，，

，

，

.