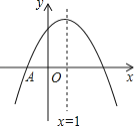Question

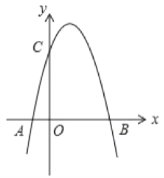
【题目】如图，二次函数的图象与轴的一个交点为，另一个交点为，且与轴相交于点

（1）则_________；点坐标为___________；

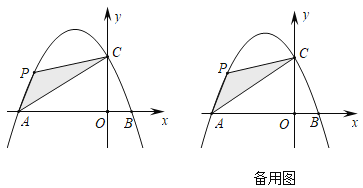
（2）在直线上方的抛物线上是否存在一点，使得它与，两点构成的三角形面积最大，若存在，求出此时点坐标；若不存在，请简要说明理由．

（3）为抛物线上一点，它关于直线的对称点为

①当四边形为菱形时，求点的坐标；

②点的横坐标为，当________时，四边形的面积最大．

Answer 1

【答案】（1）4，（0，4）；（2）存在，（2，6）；（3）①点坐标为或；②2．

【解析】

（1）用待定系数法求出抛物线解析式；

（2）先判断出面积最大时，平移直线BC的直线和抛物线只有一个交点，从而求出点M坐标；

（3）①先判断出四边形PBQC时菱形时，点P是线段BC的垂直平分线，利用该特殊性建立方程求解；

②先求出四边形PBCQ的面积与t的函数关系式，从而确定出它的最大值．

解：（1）将B（4，0）代入y＝－x2＋3x＋m，

解得，m＝4，

∴二次函数解析式为y＝－x2＋3x＋4，

令x＝0，得y＝4，

∴C（0，4），

故答案为：4，（0，4）；

（2）存在，

理由：∵B（4，0），C（0，4），

∴直线BC解析式为y＝－x＋4，

当直线BC向上平移b单位后和抛物线只有一个公共点时，△MBC面积最大，

∴，

∴x2－4x＋b＝0，

∴△＝16－4b＝0，

∴b＝4，

∴，

∴M（2，6），

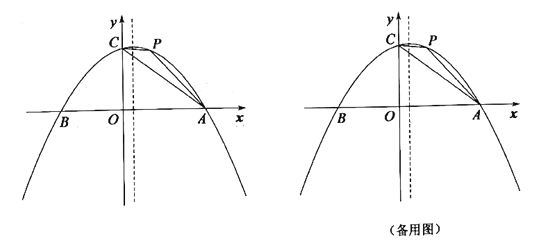
（3）①如图，

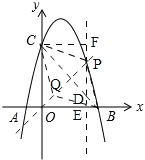
∵点P在抛物线上，

∴设P（m，－m2＋3m＋4），

当四边形PBQC是菱形时，点P在线段BC的垂直平分线上，

∵B（4，0），C（0，4）

∴线段BC的垂直平分线的解析式为y＝x，

∴m＝－m2＋3m＋4，

∴m＝1±，

∴P（1＋，1＋）或P（1－，1－），

②如图，

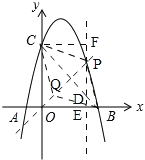
设点P（t，－t2＋3t＋4），

过点P作y轴的平行线l，过点C作l的垂线，

∵点D在直线BC上，

∴D（t，－t＋4），

∵PD＝－t2＋3t＋4－（－t＋4）

＝－t2＋4t，

BE＋CF＝4，

∴S四边形PBQC＝2S△PCB

＝2（S△PCD＋S△PBD）

＝2（PD×CF＋PD×BE）

＝4PD

＝－4t2＋16t，

∵0＜t＜4，

∴当t＝2时，S四边形PBQC最大＝16，

故答案为：2．