题目内容

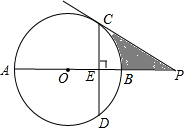如图，P是⊙O的直径AB延长线上的一点，PC切⊙O于点C，弦CD⊥AB，垂足为点E，若 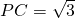$数学公式$ ，PB=1．求：
（1）⊙O的半径；
（2）CD的长；
（3）图中阴影部分的面积．

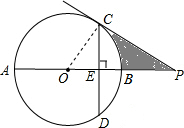解：（1）连接OC，
∵PC切⊙O于点C，
∴OC⊥PC，
设⊙O的半径为x，
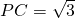∵ $\text{[math]}$ ，PB=1，
则OP=x+1，
在Rt△POC中，OC²+PC²=OP²，
∴x²+（ $\text{[math]}$ ）²=（x+1）²，
解得：x=1，
即⊙O的半径为1；

（2）∵弦CD⊥AB，
∴CE= $\text{[math]}$ CD，
∵在Rt△POC中，sin∠POC= $\text{[math]}$ = $\text{[math]}$ ，
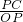∴在Rt△OCE中，CE=OC•sin∠COE= $\text{[math]}$ ，
∴CD=2CE= $\text{[math]}$ ；

（3）∵sin∠POC= $\text{[math]}$ ，
∴∠POC=60°，
∴S_阴影=S_Rt△POC-S_扇形BOC= $\text{[math]}$ PC•OC- $\text{[math]}$ = $\text{[math]}$ - $\text{[math]}$ ．
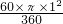分析：（1）首先连接OC，由PC切⊙O于点C，可得OC⊥PC，然后设⊙O的半径为x，由勾股定理可得方程：x²+（ $\text{[math]}$ ）²=（x+1）²，解此方程即可求得答案；
（2）由弦CD⊥AB，根据垂径定理的即可求得CD的长；
（3）由sin∠POC= $\text{[math]}$ ，可得∠POC=60°，则可由S_阴影=S_Rt△POC-S_扇形BOC求得答案．
点评：此题考查了切线的性质、垂径定理、勾股定理以及特殊角的三角函数问题．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．