题目内容
20．不透明的袋子里装有1个红球，1个白球，这些球除颜色外无其他差别，从袋子中随机摸出一个球，则摸出红球的概率是$\frac{1}{2}$．分析 用红球的数量除以球的总数量即可求得摸到红球的概率．
解答 解：∵共2个球，有1个红球，
∴P（摸出红球）=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
10．我们解一元二次方程3x2-6x=0时，可以运用因式分解法，将此方程化为3x（x-2）=0，从而得到两个一元一次方程：3x=0或x-2=0，进而得到原方程的解为x1=0，x2=2．这种解法体现的数学思想是（ ）
| A． | 转化思想 | B． | 函数思想 | C． | 数形结合思想 | D． | 公理化思想 |
11．下列说法正确的是（ ）
| A． | 1的相反数是-1 | B． | 1的倒数是-1 | C． | 1的立方根是±1 | D． | -1是无理数 |
8．
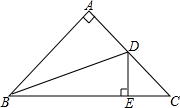如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（ ）
如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（ ）| A． | $\frac{1}{3}$ | B． | $\sqrt{2}$-1 | C． | 2-$\sqrt{3}$ | D． | $\frac{1}{4}$ |
15．已知一个单项式的系数是2，次数是3，则这个单项式可以是（ ）
| A． | -2xy2 | B． | 3x2 | C． | 2xy3 | D． | 2x3 |
12．下列运算正确的是（ ）
| A． | a+2a=3a2 | B． | 3a3•2a2=6a6 | C． | a8÷a2=a4 | D． | （2a）3=8a3 |
15．等腰△ABC中，∠A=30°，AB=4，则AB边上的高CD的长是（ ）
| A． | 2或2$\sqrt{3}$或$\frac{{\sqrt{3}}}{3}$ | B． | 2或$4\sqrt{3}$或$\frac{{\sqrt{3}}}{3}$ | C． | 2或2$\sqrt{3}$或$\frac{{2\sqrt{3}}}{3}$ | D． | 2或$4\sqrt{3}$或$\frac{2\sqrt{3}}{3}$ |