题目内容
(1)如图①,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交OC于点E。求证CD=CE。
(2)若将图①中的半径OB所在直线向上平行移动交OA于F,交⊙O于B′,其他条件不变(如图②),那么上述结论CD=CE还成立吗?为什么?

(1)证明:连结OD,则OD⊥DC,∵OA=OD, ∴∠OAD=∠ODA。
又∵∠ODA+∠EDC=90°, ∠OAD+∠AEO=90°,
∴∠EDC=∠AEO ∵∠AEO=∠CED ∴∠EDC=∠CED, ∴CE=CD
(2)结论CD=CE还成立
理由如下:连结OD,则OD⊥DC
∵OB所在直线向上平行移动,∴AF⊥FC。
证法同(1),可知CD=CE仍成立

练习册系列答案
相关题目
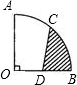 如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为
如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为
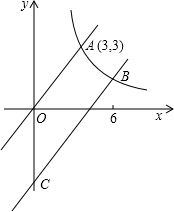 图象交于点B(6,m)与y轴交于点C,
图象交于点B(6,m)与y轴交于点C, 如图,射线OA表示的是
如图,射线OA表示的是 如图已知OA=OD,要证明△AOB≌△DOC,还应添加一个条件
如图已知OA=OD,要证明△AOB≌△DOC,还应添加一个条件 已知:如图,射线OA和点P.
已知:如图,射线OA和点P.