题目内容
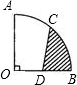 如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为
如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为 | AB |
分析:连接CO,易得∠COB=45°.作CE⊥OB于点E,那么CE=CO×sin45°=
.阴影部分面积为S扇形BOC-S△OCD,依面积公式计算即可.
| 2 |
解答: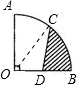 解:连接CO,易得∠COB=45°.
解:连接CO,易得∠COB=45°.
作CE⊥OB于点E,
那么CE=CO×sin45°=
.
阴影部分面积=S扇形BOC-S△OCD=
-
×1×
=
(π-
).
 解:连接CO,易得∠COB=45°.
解:连接CO,易得∠COB=45°.作CE⊥OB于点E,
那么CE=CO×sin45°=
| 2 |
阴影部分面积=S扇形BOC-S△OCD=
| 45π22 |
| 360 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:此题考查了运用切割法求图形的面积.解决本题的关键是把所求的面积转化为容易算出的面积的和或差的形式.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
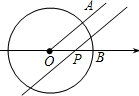 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )A、O<x≤
| ||||
B、-
| ||||
| C、-1≤x≤1 | ||||
D、x>
|
 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P(P与O不重合)在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设点P所表示的实数为x,则x的取值范围是( )
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P(P与O不重合)在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设点P所表示的实数为x,则x的取值范围是( )| A、-1≤x<0或0<x≤1 | ||||
B、0<x≤
| ||||
C、-
| ||||
D、x>
|
 12、已知如图,两同心圆中大圆的半径OA、OB交小圆于C,D,OC:CA=3:2,则弧CD和弧AB的长度比为( )
12、已知如图,两同心圆中大圆的半径OA、OB交小圆于C,D,OC:CA=3:2,则弧CD和弧AB的长度比为( ) (2012•鄂尔多斯)如图,正方形OABC的边长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
(2012•鄂尔多斯)如图,正方形OABC的边长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( ) (2013•昭通)如图所示是某公园为迎接“中国--南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
(2013•昭通)如图所示是某公园为迎接“中国--南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )