Question

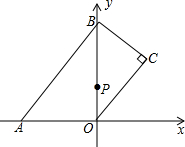
如图，将以点A为直角顶点腰长为2的等腰直角三角形ABC沿直线BC平移到△A₁B₁C₁，使点B₁与点C重合，连接A₁B，则A₁B=________．

Answer 1

2
分析：过点A₁作A₁D⊥B₁C₂于D，根据等腰直角三角形的性质求出斜边BC的长，根据平移的性质可得B₁C₁=BC，根据等腰直角三角形的性质可得A₁D=B₁D=B₁C₁，然后求出BD，再利用勾股定理列式计算即可求出A₁B．
解答：解：如图，过点A₁作A₁D⊥B₁C₂于D，
∵等腰直角三角形的腰长为2，
∴BC=×2=4，
∵△ABC沿直线BC平移到△A₁B₁C₁，
∴B₁C₁=BC，
∴A₁D=B₁D=B₁C₁=×4=2，
∴BD=BC+B₁D=4+2=6，
在Rt△A₁BD中，A₁B===2．
故答案为：2．
点评：本题考查了平移的性质，主要利用了等腰直角三角形的性质，作辅助线构造出边A₁B所在的直角三角形是解题的关键，也是本题的难点．