题目内容
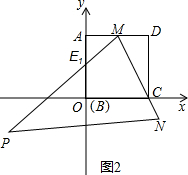
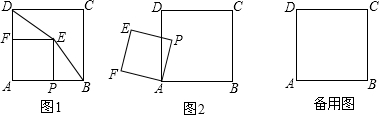
如图①,将一边AB长为4cm的矩形框架ABCD与两直角边分别为4cm、3cm的直角三角形框架拼成直角梯形ABED.动点P,Q同时从点E出发,点P沿E→D→A方向以每秒3cm的速度运动,点Q沿E→B→A方向以每秒4cm的速度运动.而当点P到达点A时,点Q也正好到达点A.设P,Q同时从点E出发时,经过的时间为t秒.

(1)分别求出梯形中DE,AD的长度;
(2)当t=
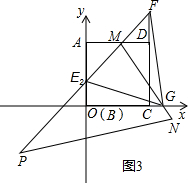
时,求△EPQ的面积,并直接写出此时△EPQ的形状(如图②);
(3)在点P,Q的运动过程中,是否存在某一时刻,使得四边形APEQ是梯形?若存在,请求出相应的t的值;若不存在,请说明理由.

(1)分别求出梯形中DE,AD的长度;
(2)当t=
| 7 | 4 |
(3)在点P,Q的运动过程中,是否存在某一时刻,使得四边形APEQ是梯形?若存在,请求出相应的t的值;若不存在,请说明理由.
分析:(1)先在直角△DCE中利用勾股定理求出DE的长,设AD=x,再根据“动点P,Q同时从点E出发,点P沿E→D→A方向以每秒3cm的速度运动,点Q沿E→B→A方向以每秒4cm的速度运动.而当点P到达点A时,点Q也正好到达点A”列出关于x的方程,解方程即可;
(2)△EPQ的面积=S梯形ABED-S△APQ-S△BQE-S△DPE,根据两边对应成比例且夹角相等的两三角形相似证明△APQ∽△BQE,由相似三角形对应角相等及直角三角形两锐角互余得出∠AQP+∠BQE=90°,进而得出△EPQ是直角三角形;
(3)根据点P和点Q的运动速度及运动路径,可分三种情况进行讨论:①0≤t≤1;②1<t≤
;③
<t≤2.
(2)△EPQ的面积=S梯形ABED-S△APQ-S△BQE-S△DPE,根据两边对应成比例且夹角相等的两三角形相似证明△APQ∽△BQE,由相似三角形对应角相等及直角三角形两锐角互余得出∠AQP+∠BQE=90°,进而得出△EPQ是直角三角形;
(3)根据点P和点Q的运动速度及运动路径,可分三种情况进行讨论:①0≤t≤1;②1<t≤
| 5 |
| 3 |
| 5 |
| 3 |
解答: 解:(1)如图①.
解:(1)如图①.
在直角△DCE中,∵∠DCE=90°,DC=AB=4cm,CE=3cm,
∴DE=
=5cm;
设AD=xcm,则BC=xcm,
由题意,
=
,
解得x=1,
即AD=1cm;
(2)如图②.
当t=
时,BQ=4×
-1-3=3,PD=3×
-5=
,
∴AQ=1,AP=
,
∴△EPQ的面积=S梯形ABED-S△APQ-S△BQE-S△DPE
=
(1+4)×4-
×
×1-
×4×3-
×
×4
=10-
-6-
=
(cm2);
∵AP:BQ=
:3=1:4,AQ:BE=1:4,
∴AP:BQ=AQ:BE.
∵在△APQ与△BQE中,
,
∴△APQ∽△BQE,
∴∠AQP=∠BEQ,
∵∠BEQ+∠BQE=90°,
∴∠AQP+∠BQE=90°,
∴∠PQE=90°,
∴△EPQ是直角三角形;
 (3)在点P,Q的运动过程中,存在时刻t,能够使得四边形APEQ是梯形.
(3)在点P,Q的运动过程中,存在时刻t,能够使得四边形APEQ是梯形.
分三种情况讨论:
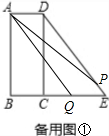
①当0≤t≤1时,点Q在EB上,点P在ED上,如备用图①;
PE=3t,QE=4t,BQ=4-4t.
若四边形APEQ是梯形,则PE∥AQ,
又∵AD∥QE,
∴四边形ADEQ是平行四边形,
∴QE=AD,即4t=1,
解得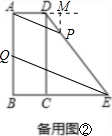 t=
t=
;
②当1<t≤
时,点Q在AB上,点P在ED上,如备用图②;
若四边形APEQ是梯形,则AP∥QE.
过点P作PM⊥AD于M,则BQ=4t-4,BE=4,EP=3t,DP=5-3t.
∵△PDM∽△DEC,
∴(5-3t):5=DM:3=PM:4,
∴DM=
(5-3t),PM=
(5-3t),
∵△AMP∽△EBQ,
∴AM:EB=PM:QB,即[1+
(5-3t)]:4=
(5-3t):(4t-4),
化简整理得,9t2-41t+40=0,
 解得t=
解得t=
.
∵
>
,舍去,
∴t=
;
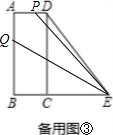
③当
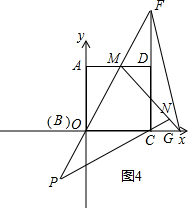
<t≤2时,点Q在AB上,点P在AD上,如备用图③,
显然四边形APEQ的两组对边都不平行,此时四边形APEQ不可能为梯形.
综上可知,在点P,Q的运动过程中,存在时刻t=
或t=
,使得四边形APEQ是梯形.
 解:(1)如图①.
解:(1)如图①.在直角△DCE中,∵∠DCE=90°,DC=AB=4cm,CE=3cm,
∴DE=
| DC2+CE2 |
设AD=xcm,则BC=xcm,
由题意,
| 4+x+3 |
| 4 |
| x+5 |
| 3 |
解得x=1,
即AD=1cm;
(2)如图②.
当t=
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 1 |
| 4 |
∴AQ=1,AP=
| 3 |
| 4 |
∴△EPQ的面积=S梯形ABED-S△APQ-S△BQE-S△DPE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
=10-
| 3 |
| 8 |
| 1 |
| 2 |
=
| 25 |
| 8 |
∵AP:BQ=
| 3 |
| 4 |
∴AP:BQ=AQ:BE.
∵在△APQ与△BQE中,
|
∴△APQ∽△BQE,
∴∠AQP=∠BEQ,
∵∠BEQ+∠BQE=90°,
∴∠AQP+∠BQE=90°,
∴∠PQE=90°,
∴△EPQ是直角三角形;
 (3)在点P,Q的运动过程中,存在时刻t,能够使得四边形APEQ是梯形.
(3)在点P,Q的运动过程中,存在时刻t,能够使得四边形APEQ是梯形.分三种情况讨论:
①当0≤t≤1时,点Q在EB上,点P在ED上,如备用图①;
PE=3t,QE=4t,BQ=4-4t.
若四边形APEQ是梯形,则PE∥AQ,
又∵AD∥QE,
∴四边形ADEQ是平行四边形,
∴QE=AD,即4t=1,
解得
 t=
t=| 1 |
| 4 |
②当1<t≤
| 5 |
| 3 |
若四边形APEQ是梯形,则AP∥QE.
过点P作PM⊥AD于M,则BQ=4t-4,BE=4,EP=3t,DP=5-3t.
∵△PDM∽△DEC,
∴(5-3t):5=DM:3=PM:4,
∴DM=
| 3 |
| 5 |
| 4 |
| 5 |
∵△AMP∽△EBQ,
∴AM:EB=PM:QB,即[1+
| 3 |
| 5 |
| 4 |
| 5 |
化简整理得,9t2-41t+40=0,
 解得t=
解得t=41±
| ||
| 18 |
∵
41+
| ||
| 18 |
| 5 |
| 3 |
∴t=
41-
| ||
| 18 |
③当
| 5 |
| 3 |
显然四边形APEQ的两组对边都不平行,此时四边形APEQ不可能为梯形.
综上可知,在点P,Q的运动过程中,存在时刻t=
| 1 |
| 4 |
41-
| ||
| 18 |
点评:本题是相似形综合题,其中涉及到矩形的性质,勾股定理,三角形的面积,相似三角形的判定与性质,梯形的判定与性质,(3)中进行分类讨论是解题的关键.

练习册系列答案
相关题目
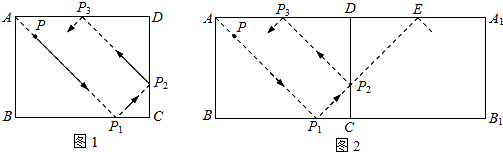
 60°,延长EF交CB的延长线于点G.
60°,延长EF交CB的延长线于点G.