题目内容
若方程（m+2）x2-4x+5=0无实根，则m的取值范围为 ．
考点：根的判别式
专题：
分析：由已知条件可得：判别式△＜0，这样解不等式即可求出m的取值范围．
解答：解：∵关于x的方程（m+2）x2-4x+5=0无实根，
∴△=（-4）2-4（m+2）×5＜0，
整理 得-5m-6＜0，
解得 m＞-
．
故答案是：m＞-
．
∴△=（-4）2-4（m+2）×5＜0，
整理 得-5m-6＜0，
解得 m＞-
| 6 |
| 5 |
故答案是：m＞-
| 6 |
| 5 |
点评：本题考查了一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
相关题目
在分别标有号码2、3、4、…10的9个球中，随机取出两个球，记下它们的标号，则较大标号被较小标号整除的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
当a=-2时，下列多项式的值为正数的是（ ）
| A、-a-4 |
| B、-3+a2 |
| C、2a-1 |
| D、a2-4 |
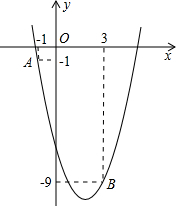如图，已知二次函数y=ax2-4x+c的图象经过点A和点B．