题目内容
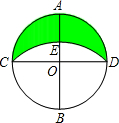 如图,⊙O的半径为6,直径AB⊥CD,以B为圆心,BC长为半径作
如图,⊙O的半径为6,直径AB⊥CD,以B为圆心,BC长为半径作 ,则
,则 与
与 围成的新月形ACED(阴影部分)的面积为________.
围成的新月形ACED(阴影部分)的面积为________.
36
分析:连BC、BD,由直径AB⊥CD,则△BOD、△ODB都为等腰直角三角形,则BC= OB=6
OB=6 ,∠CBD=90°,利用S弓形CED=S扇形CBD-S△BCD和扇形的面积公式计算得到
,∠CBD=90°,利用S弓形CED=S扇形CBD-S△BCD和扇形的面积公式计算得到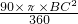 -
- CD•BO=18π-36,然后再利用S阴影部分=S半圆ACD-S弓形CED进行计算即可.
CD•BO=18π-36,然后再利用S阴影部分=S半圆ACD-S弓形CED进行计算即可.
解答:连BC、BD,如图,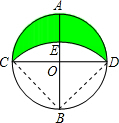
∵直径AB⊥CD,
∴△BOD为等腰直角三角形,
∴BC= OB=6
OB=6 ,∠CBD=90°,
,∠CBD=90°,
∴S弓形CED=S扇形CBD-S△BCD
=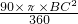 -
- CD•BO
CD•BO
=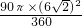 -
- ×12×6
×12×6
=18π-36,
∴S阴影部分=S半圆ACD-S弓形CED= ×π×62-(18π-36)=36.
×π×62-(18π-36)=36.
故答案为36.
点评:本题考查了扇形面积公式:扇形的面积S= (n为圆心角的度数,R为圆的半径).也考查了等腰直角三角形的性质.
(n为圆心角的度数,R为圆的半径).也考查了等腰直角三角形的性质.
分析:连BC、BD,由直径AB⊥CD,则△BOD、△ODB都为等腰直角三角形,则BC=
 OB=6
OB=6 ,∠CBD=90°,利用S弓形CED=S扇形CBD-S△BCD和扇形的面积公式计算得到
,∠CBD=90°,利用S弓形CED=S扇形CBD-S△BCD和扇形的面积公式计算得到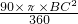 -
- CD•BO=18π-36,然后再利用S阴影部分=S半圆ACD-S弓形CED进行计算即可.
CD•BO=18π-36,然后再利用S阴影部分=S半圆ACD-S弓形CED进行计算即可.解答:连BC、BD,如图,

∵直径AB⊥CD,
∴△BOD为等腰直角三角形,
∴BC=
 OB=6
OB=6 ,∠CBD=90°,
,∠CBD=90°,∴S弓形CED=S扇形CBD-S△BCD
=
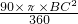 -
- CD•BO
CD•BO=
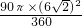 -
- ×12×6
×12×6=18π-36,
∴S阴影部分=S半圆ACD-S弓形CED=
 ×π×62-(18π-36)=36.
×π×62-(18π-36)=36.故答案为36.
点评:本题考查了扇形面积公式:扇形的面积S=
 (n为圆心角的度数,R为圆的半径).也考查了等腰直角三角形的性质.
(n为圆心角的度数,R为圆的半径).也考查了等腰直角三角形的性质. 
练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为