题目内容
如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=
 AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当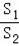
 =
=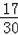
 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)


【考点】四边形综合题.
【专题】几何综合题.
【分析】(1)先求证△EFO≌△BGO,可得EF=BG,再根据△BOF≌△EOF,可得EF=BF;即可证明四边形BFEG为菱形;
(2)根据菱形面积不同的计算公式(底乘高和对角线乘积的一半两种计算方式)可计算FG的长度;
(3)根据菱形面积底乘高的计算方式可以求出BG长度,根据勾股定理可求出AF的长度,即可求出ED的长度,即可计算n的值.
【解答】解:(1)∵AD∥BC,
∴∠EFO=∠BGO,
∵FG为BE的垂直平分线,
∴BO=OE;
∵在△EFO和△BGO中,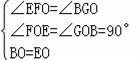
 ,
,
∴△EFO≌△BGO,
∴EF=BG,
∵AD∥BC,
∴四边形BGEF为平行四边形;
∵在△BOF和△EOF中,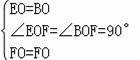
 ,
,
∴△BOF≌△EOF,
∴EF=BF,
∵邻边相等的平行四边形为菱形,
∴四边形BGEF为菱形.
(2)当AB=a,n=3时,AD=2a,AE=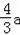
 ,
,
根据勾股定理可以计算BE=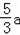
 ,
,
∵AF=AE﹣EF=AE﹣BF,在Rt△ABF中AB2+AF2=BF2,计算可得AF=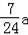
 ,EF=
,EF=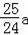
 ,
,
∵菱形BGEF面积=
 BE•FG=EF•AB,计算可得FG=
BE•FG=EF•AB,计算可得FG=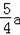
 .
.
(3)设AB=x,则DE=
 ,
,
S1=BG•AB,S2=BC•AB
当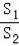
 =
=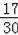
 时,
时,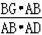
 =
=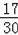
 ,可得BG=
,可得BG=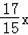
 ,
,
在Rt△ABF中AB2+AF2=BF2,计算可得AF=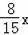
 ,
,
∴AE=AF+FE=AF+BG=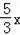
 ,DE=AD﹣AE=
,DE=AD﹣AE=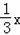
 ,
,
∴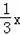
 =
=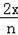
 ,
,
∴n=6.
【点评】牢记菱形的底乘高和对角线求面积的计算公式,熟练运用勾股定理才能解本题.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案

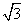 ≈1.732)
≈1.732)

 +
+


 +
+

