Question

已知，在△ABC中，AD为∠BAC的平分线，点E在BC的延长线上，且∠EAC＝∠B，以DE为直径的半圆交AD于点F，交AE于点M．

（1）判断AF与DF的数量关系，并说明理由；

（2）只用无刻度的直尺画出△ADE的边DE上的高AH；

（3）若EF＝4，DF＝3，求DH的长．

 

   

Answer 1

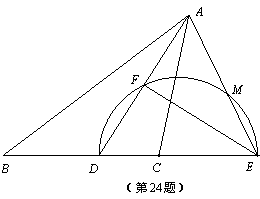解：（1）．

理由如下：

∵AD平分，∴∠BAD=∠CAD．

又∵∠B=∠CAE，∴∠BAD+∠B=∠CAD+∠CAE．

即∠ADE=∠DAE ，

∴．

∵DE是直径，∴EF⊥AD，

∴．    

（2）画图正确…    

（3）由勾股定理得

∵∠ADH=∠EDF，∠AHD=∠DFE=90°，

∴△ADH∽△EDF．

∴．∴．