题目内容
(2012•高邮市一模)一辆货车在A处加满油后匀速行驶,下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
(1)求y与x之间的函数关系式;
(2)求货车行驶4.2小时到达B处时油箱内的余油量.
| 行驶时间x(时) | 0 | 1 | 2 | 2.5 |
| 余油量y(升) | 100 | 80 | 60 | 50 |
(2)求货车行驶4.2小时到达B处时油箱内的余油量.
分析:(1)根据图表上点的坐标得出y与x之间的函数关系式,进而判定y与x的函数关系;
(2)利用当x=4.2时,由y=-20x+100可得y=16,即可得出答案.
(2)利用当x=4.2时,由y=-20x+100可得y=16,即可得出答案.
解答:解:(1)设y与x之间的关系为一次函数,其函数表达式为y=kx+b,
将(0,100),(1,80)代入上式得:
,
解得:
,
则y=-20x+100,
验证:当x=2时,y=-20×2+100=60,符合一次函数y=-20x+100;
当x=2.5时,y=-20×2.5+100=50,也符合一次函数y=-20x+100.
则可用一次函数y=-20x+100表示其变化规律,
而不用反比例函数、二次函数表示其变化规律
y与x之间的关系是一次函数,其函数表达式为:y=-20x+100;
(2)当x=4.2时,由y=-20x+100可得y=16,
即货车行驶到B处时油箱内余油16升.
将(0,100),(1,80)代入上式得:
|
解得:
|
则y=-20x+100,
验证:当x=2时,y=-20×2+100=60,符合一次函数y=-20x+100;
当x=2.5时,y=-20×2.5+100=50,也符合一次函数y=-20x+100.
则可用一次函数y=-20x+100表示其变化规律,
而不用反比例函数、二次函数表示其变化规律
y与x之间的关系是一次函数,其函数表达式为:y=-20x+100;
(2)当x=4.2时,由y=-20x+100可得y=16,
即货车行驶到B处时油箱内余油16升.
点评:此题主要考查了一次函数的应用以及待定系数法求一次函数解析式,根据已知得出y与x的函数关系式是解题关键.

练习册系列答案
相关题目
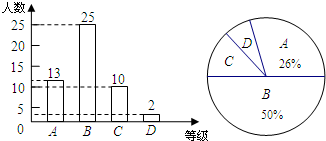 (2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空:
(2012•高邮市一模)学校以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息填空: (2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为
(2012•高邮市一模)如图,DE是△ABC的中位线,M是DE的中点,若△ABC的面积为48cm2,则△DMN的面积为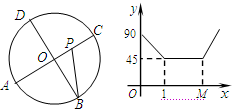 (2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为
(2012•高邮市一模)如图,A、B、C、D是⊙O四等分点,动点P沿O-C-D-O路线作匀速运动,设运动时间为xs,∠APB=y°,右图表示y与x之间函数关系,则点M的横坐标为