题目内容
如图,在△ABC中,∠ACB=90°,AB= 5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
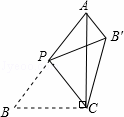
1. 解:在Rt△ABC中,由勾股定理可知:AC= =
= =4,
=4,
由轴对称的性质可知:BC=CB′=3,
∵CB′长度固定不变,
∴当AB′+CB′有最小值时,AB′的长度有最小值.
根据两点之间线段最短可知:A、B′、C三点在一条直线上时,AB′有最小值,
∴AB′=AC﹣B′C=4﹣3=1.

练习册系列答案
相关题目
某一天,蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子,到菜市场去卖,黄瓜和茄子当天的批发价与零售价如下表所示:
| 品名 | 黄瓜 | 茄子 |
| 批发价(元/千克) | 3 | 4 |
| 零售价(元/千克) | 4 | 7 |
当天他卖完这些黄瓜和茄子共赚了90元,这天他批发的黄瓜和茄子分别是多少千克?
 0),二次函数y=
0),二次函数y= x2+bx+c的图象抛物线经过A,C两点.
x2+bx+c的图象抛物线经过A,C两点.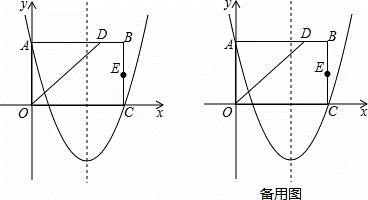
 =±2
=±2 = .
= .
