题目内容
15.已知关于x的一元二次方程x2-3x+m-3=0,若此方程的两根的倒数和为1,求m的值.分析 设方程的两个根分别为α、β,由根与系数的关系可得出α+β=3、αβ=m-3,结合$\frac{1}{α}$+$\frac{1}{β}$=1可得出$\frac{3}{m-3}$=1,解之即可得出m的值,再根据根的判别式即可得出△=21-4m≥0,解之即可得出m的取值范围,由此即可确定m无解.
解答 解:设方程的两个根分别为α、β,
∴α+β=3,αβ=m-3.
∵$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{αβ}$=$\frac{3}{m-3}$=1,
∴m=6,
经检验,m=6是分式方程$\frac{3}{m-3}$=1的解.
∵方程x2-3x+m-3=0有两个实数根,
∴△=(-3)2-4(m-3)=21-4m≥0,
∴m≤$\frac{21}{4}$,
∴m=6舍去.
∴m无实数根.
点评 本题考查了根与系数的关系以及根的判别式,利用根与系数的关系结合$\frac{1}{α}$+$\frac{1}{β}$=1找出$\frac{3}{m-3}$=1是解题的关键.

练习册系列答案
相关题目
5.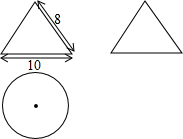 如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )| A. | 40πcm2 | B. | 65πcm2 | C. | 80πcm2 | D. | 105πcm2 |
6.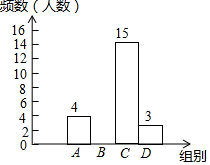 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
(1)图中a=4,这次比赛成绩的众数落在C组;
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
 为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题.
为丰富学生的校园生活,某校举行“与爱同行”朗诵比赛,赛后整理参赛同学的成绩,绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题. | 组别 | 成绩x(分) | 频数(人数) |
| A | 8.0≤x<8.5 | a |
| B | 8.5≤x<9.0 | 8 |
| C | 9.0≤x<9.5 | 15 |
| D | 9.5≤x<10 | 3 |
(2)请补全频数分布直方图;
(3)学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛,并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条,小军先选,他从中随机选取一件上衣和一条裤子搭配成一套衣服,请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率.
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等腰直角三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 矩形 |
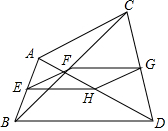 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.